Пусть необходимо извлечь выборку объёма n= 25 из нормально распределённой случайной величины x сматематическим ожиданием mx=10 идисперсией 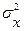 =4. Хотим определить интервал, в котором с вероятностью 95% заключено выборочное среднее значение
=4. Хотим определить интервал, в котором с вероятностью 95% заключено выборочное среднее значение  .
.
Очевидно, что выборочное среднее значение  представляет собой одно значение, выбранное из нормально распределённой случайной величины x сосредним значением m
представляет собой одно значение, выбранное из нормально распределённой случайной величины x сосредним значением m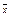 = 10и
= 10и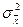 =
=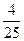 .
.
Для того чтобы найти интервал, в котором с вероятностью 95% заключено выборочное среднее значение  , зададимся границами этого интервала такими, что вероятность попадания
, зададимся границами этого интервала такими, что вероятность попадания  слева от интервала составляет 2,5% и справа - 2,5%, то есть вероятность нахождения случайной величины x вне интервала равна 5%.
слева от интервала составляет 2,5% и справа - 2,5%, то есть вероятность нахождения случайной величины x вне интервала равна 5%.
Из формулы P ( >
> 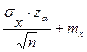 )=a можно найти вероятность попадания:
)=a можно найти вероятность попадания:
P (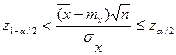 )=1-a
)=1-a
P (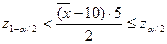 )=1-a
)=1-a
Из таблиц нормального распределения для a= 0,05 находим 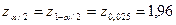 .
.
Таким образом, границами будут значения:
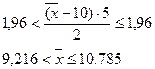
Поэтому с вероятностью, равной 95%, выборочное среднее значение  будет находиться в пределах от 9,216 до 10,785.
будет находиться в пределах от 9,216 до 10,785.
Рассмотрим случай, когда случайная величина x распределена по закону, отличному от нормального. Из центральной предметной теоремы вытекает, что с увеличением объёма выборки n выборочное распределение среднего значения выборки  приближается к нормальному распределению независимо от вида распределения исходной случайной величины x. Сточки зрения практики, предположение о нормальности выборочного распределения становится приемлемым во многих случаях при n=4 и хорошо оправдывается при n= 10 иболее. Следовательно, при достаточно больших объёмах выборки в качестве выборочного распределения среднего значения выборки для любой случайной величины x можно использовать выражение (*), независимо от закона распределения этой случайной величины.
приближается к нормальному распределению независимо от вида распределения исходной случайной величины x. Сточки зрения практики, предположение о нормальности выборочного распределения становится приемлемым во многих случаях при n=4 и хорошо оправдывается при n= 10 иболее. Следовательно, при достаточно больших объёмах выборки в качестве выборочного распределения среднего значения выборки для любой случайной величины x можно использовать выражение (*), независимо от закона распределения этой случайной величины.
2.Распределение выборочного среднего при неизвестной дисперсии.
Рассмотрим n – объём выборки независимых наблюдений случайной величины x.
случайная величина x распределена по нормальному закону сматематическим ожиданием m x инеизвестной дисперсией 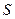 . Укажем распределение выборочного среднего.
. Укажем распределение выборочного среднего.
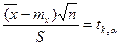
Эта величина подчиняется распределениюСтьюдента с 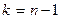 степенями свободы. Отсюда вытекает следующее вероятностное утверждение относительно
степенями свободы. Отсюда вытекает следующее вероятностное утверждение относительно  до извлечения выборки.
до извлечения выборки.
P ( >
>  )=a (**).
)=a (**).
Значение 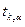 - это квантиль распределения Стьюдента уровня a.
- это квантиль распределения Стьюдента уровня a.
 2014-02-02
2014-02-02 957
957








