Регулярные множества и регулярные выражения

Определим еще некоторый класс языков — регулярных множеств. Соотношение его с классом А-языков определим позднее.

Пусть V_T конечный алфавит. Регулярные множества в алфавите V_T определяются рекурсивно:

1) Æ - регулярное множество;

2) {l} - регулярное множество;

3) {a} регулярное множество для любого aÎV_T;

4) если P и Q - регулярные множества, то таковы также и множества: PÈQ, PQ, P*;

5) никаких других регулярных множеств нет.

По-другому можно определить регулярное множество как такое, которое можно получить из Æ, {l}, {a} и множеств, полученных на предыдущих шагах, путем конечного числа при­менений операций " È ", " × " и "*".

Определим теперь специальную нотацию для задания регулярных множеств.

Регулярные выражения в алфавите V_T и регулярные множества, которые они обозначают, определяются рекурсивно:

1) 0 - регулярное выражение, обозначающее регулярное множество Æ.

2)1 - регулярное выражение, обозначающее регулярное множество {l},

3) если aÎ V_T; то a - регулярное выражение, обозначающее регулярное множество {a};

4) если p и q - регулярные выражения, обозначающие регулярные множества P и Q то:

a) (p+q) - регулярное выражение, обозначающее регулярное множество PÈQ,

б) (pq) - регулярное выражение, обозначающее регулярное множество PQ,

в) (p*) - регулярное выражение, обозначающее регулярное множество P*;

5) никаких других регулярных выражений нет.

Как обычно, когда можно опустить лишние скобки без по­тери однозначности чтения, мы будем это делать. Так, 0+110* обозначает (0+((11)(0)*)). Мы будем придерживаться соглашения, что * обладает наивысшим приоритетом, затем • и, наконец, +.

Очевидно, что для каждого регулярного множества можно найти регулярное выражение, его обозначающее, и наоборот. К сожалению, как мы увидим дальше, одному и тому же регулярному множеству может соответствовать бесконечно много регулярных выражений.

Будем говорить, что регулярные выражения равны (обозначается значком =), если они обозначают одно и то же регу­лярное множество.

Запишем основные алгебраические тождества для регулярных выражений. Часть из них мы уже знаем, остальные легко доказываются. Если a, b, g - регулярные выражения, то:

1. a+a=a;

2. a+b=b+a;

3. a(bg)=(ab)g;

4. a+(b+g)=(a+b)+g;

5. a1=1a=a;

6. a0=0a=0;

7. (a+b)g=ag+bg;

8. a(b+g)=ab+ag;

9. a*=a+a*;

10. (a*)*=a*;

11. a*a* = a*

12. a*a =aa*

13. a+0=a

14. 1*=1

15. 0*=1;

16. (ab)*a=a(ba)*;

17. (a*b)*a*=(a+b)*=(a* +b*)*;

18. (a*b)*=(a+b)*b+1;

19. (ab*)*=a(a+b)* +1;

20. Если a = b*g, то a=b*a+g;

21. Если 1Ïb и a=ba+g, то a=b*g.

Последнее тождество является основным при решении уравнений.

Теорема (Клини). Каждому А-языку над V соответствует регулярное выражение над V. Каждому регулярному выражению над V соответствует А-язык.

Идея доказательства:

L – регулярное множество Þ L – А-язык.

- регулярное множество (грамматика с пустым множеством правил);

l - регулярное множество (S®l);

аÎ V_T - регулярное множество (S®а);

если P, Q регулярные множества, то PÈQ, P Q, P* - так же регулярные множества (легко показать через соединение двухполюсников, порождающих языки, соответствующие P и Q.

L - А-язык Þ L – регулярное множество.

Пусть есть А-грамматика G=< V_T,V_N, S, R>,

A_i ® a₁½ a₂½… a_k½ b₁A_j1½ b₂A_j2½ …½ b_mA_jm

где a_s, b_qÎV_T, A_jsÎV_N. Обозначим X_i - язык, порождаемый грамматикой G_i в которой в качестве начального символа выбран символ А_i. Тогда указанные правила эквивалентны следующему уравнению:

X_i = a₁ + a₂ + …+ a_k + b₁X_j1 + b₂ X_j2 + … + b_m X_jm.

Действительно, если X_i обозначает язык, порождаемый грамматикой G_i, когда A_i - начальный символ, то, так как возможны выводы A_i ® a₁, A_i ® a₂, A_i ® a_k, мо­жем написать, что a₁, a₂,…, a_kÎ X_i и, следовательно, X_i = a₁ + a₂ +…+ a_k +… С другой стороны, пусть A_jkÞx_jk, т.е. x_jkÎX_jk, тогда возможен вывод A_i Þ⁺ b_kA_jk Þ⁺ b_kx_jk. Следовательно, b_kx_jkÎX_i и это верно для любой цепочки x_jkÎX_jk. Поэтому, дополняя предыдущую запись X_i, можем написать:

X_i = a₁ + a₂ + …+ a_k + b₁X_j1 + b₂ X_j2 + … + b_m X_jm.

Полное доказательство проводится индукцией по числу правил грамматики.

Как по регулярному выражению построить А-грамматику?

Конкатенация моделируется последовательным соединением двухполюсников, + - параллельным соединением, * - l- замыканием. Т.о., последовательно выполняя операции, получим двухполюсники, соответствующие регулярному выражению. Построенные двухполюсники можно затем упростить.

Например, регулярным выражениям (a+b)c, (a+b)*c, (ab+bc)*(ab+c) будут соответствовать диаграммы, представленные на рис. 21 а, б, в соответственно.

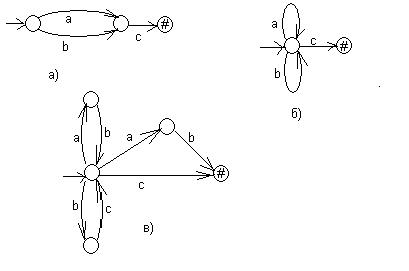
Рис.21

Обратная задача:

есть А-грамматика. Надо найти язык, порождаемый этой грамматикой, записанный в виде регулярного выражения.

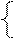
Например, имеется А-грамматика G₁₂ с правилами:

A® a A½bB

B ® b B ½ c

Обозначим язык, порождаемый грамматикой с начальным символом A - X_a, и язык, порождаемый грамматикой с начальным символом B – X_b.

Тогда соответствующие уравнения примут вид:

X_a = a X_a + b X_b

X_b = b X_b + c

Система уравнений может иметь бесконечно много решений, нас интересует минимальное по мощности решение.

Систему уравнений с регулярными коэффициентами назо­вем стандартной над множествомнеизвестных D={X1,X2,...X_n}, если она имеет вид

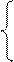X₁ = a₁₀ + a₁₁ X₁ + a₁₂ X₂ +... + a_1n X_n;

X₂ = a₂₀ + a₂₁ X₁ + a₂₂ X₂ +... + a_2n X_n;

…

X_n = a _n0 + a_n1 X₁ + a_n2 X₂ +... + a_nn X_n;

где все a _{i j} - регулярные выражения. Если какое-либо i-оеуравнение не содержит переменную X_j, то достаточно положить соответствующий коэффициент a _{i j} = 0, если a _{i j} =1, то его можно не писать.

В общем случае система уравнений имеет вид:

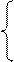x₁= f₁(x₁, x₂,…,x_n)

x₂= f₂(x₁, x₂,…,x_n)

….

x_n= f_n(x₁, x₂,…,x_n)

Где f_{i -} конечная функция, x_j – конечное множество строк над V_T, на множестве x₁, x₂,…,x_n определены операции объединения и конкатенации. Обозначим x₁, x₂,…,x_n как Х, а систему X =F(X). Решение системы S =(S1,S2,…Sn) – совокупность подмножеств V_T, такая, что S =F(S).

Определим S Í T = _Df S₁ÍT₁, S₂ ÍT₂, …, S_n Í T_n.

Теорема. Система уравнений X =F(X) имеет решение S =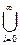Fⁱ(Æ). Если S₁ – другое решение, то SÍS₁.

Определение: Говорим, что функция F: P(A)´P(A)® P(A) монотонно возрастает, если из A₁ÍB₁ и A₂ ÍB₂ следует, что F(A₁,A₂) Í F(B₁,B₂).

Лемма: Операция конкатенации – монотонно возрастающая функция.

Очевидно, что операция объединения так же является монотонно возрастающей функцией.

Доказательство теоремы:

Т.к. Æ = (Æ,Æ, …,Æ), то Æ ÍF(Æ). Легко показать, что если A Í B, то F(A) Í F(B). Поэтому F(Æ)ÍF(F(Æ)) и т.д. Получаем возрастающую последовательность: Æ Í F(Æ) Í F²(Æ) Í F³(Æ) Í…

Пусть S =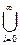Fⁱ(Æ). Тогда S =F(S). Если T - некоторое другое решение, то T = F(T), но Æ Í T, значит, F(Æ)Í F(T)= T. Очевидно, что по индукции можно доказать, что Fⁱ(Æ)Í T для всех i, следовательно, 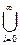Fⁱ(Æ)Í T.

Пример: Рассмотрим систему

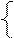
X_a = a X_a + b X_b

X_b = b X_b + c

Для удобства работы обозначим X_a – x, X_b – y.

f₁(x,y)= ax + y;

f₂(x,y)=by+c;

f1(Æ,Æ)=Æ; f2(Æ,Æ)=c;

f1(Æ,c)=bc; f2(Æ,c)=bc+c;

f1(bc,bc+c)= abc+b(b+l)c f2(bc,bc+c)=(b2+b+l)c

f₁(abc+b(b+l)c, (b²+b+l)c) =(a+l)ab(bc+c)+b(b+l)²c

f₂(abc+b(b+l)c, (b²+b+l)c) = (b³+b²+b+l)c

f₁((a+l)ab(bc+c)+b(b+l)²c, (b³+b²+b+l)c)= (a+l)³ab(bc+c)+b(b³+b²+b+l)c

Откуда получаем

y=b*c

x=a*bb*c

Тем не менее основным способом решения стандартной системы уравнений - ме­тод последовательного исключения неизвестных, подобным методу Гаусса. Покажем это на этом же примере.

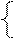X_a = a X_a + b X_b

X_b = b X_b + c

Из тождества 21 получаем

X_b=b*c

X_a = a X_a + b b*c= a*bb*c

Таким образом, существуют следующие основные способы задания А-языков:

А-грамматика.

Конечные лингвистические автоматы.

Стандартная система уравнений.

Регулярное выражение.