Синтаксический анализ для КС-языков

Может рассматриваться синтаксический анализ в широком или же узком смысле. Синтаксический анализ в узком смысле – по цепочке определить её структуру (или же построить синтаксическое дерево). Т.Е. задача сводится к построению вывода данной цепочки в данной грамматике.

Синтаксический анализ в широком смысле – определение, может ли данная цепочка быть построена с использованием данной грамматики. Это в общем случае гораздо более сложная задача.

Существующие алгоритмы синтаксического анализа классифицируются по:

1. Cпособу построения вывода: нисходящие, восходящие, смешанные
2. Способу выбора альтернативы: детерминированные и недетерминированные. В первом случае на каждом шаге выбирается правильная альтернатива, во втором – альтернатива выбирается наугад.
3. Способу возврата (для недетерминированного выбора альтернативы): разбор с быстрым или медленным возвратом.
4. По степени доступности цепочки: или цепочка доступна вся сразу, или же читается слева направо посимвольно (при этом доступно для анализа определенное число символов).

Обычно рассматривается нисходящий или восходящий разбор при чтении цепочки слева направо.

Типовая задача синтаксического анализа:

Имеется активный нетерминал S и множество альтернатив:

S®j₁½j₂½¼½j_k и текущее состояние анализируемой цепочки Y. Пусть выбрана альтернатива S®X₁X₂…X_n, X_iÎV_NÈV_T, при iÎ[1,n]. Если X₁Î V_T, то он должен совпадать с первым символом цепочки Y. Если совпадает, то укорачиваем цепочку на этот символ и переходим к X₂. Если не совпадает, то переходим к другой альтернативе.

Если же X_iÎV_N, тогда из X_i необходимо вывести какое-нибудь начало цепочки Y. Если из X_i нельзя вывести никакое начало цепочки Y, то возможны 2 варианта:

1). Сразу перейти к X_i-1 и попытаться вывести из X_i-1 другое начало и т.д. (получаем полный перебор вариантов вывода) – разбор с медленным возвратом.

2). Сразу отказаться от альтернативы S®X₁X₂…X_n (разбор с быстрым возвратом).

Очевидно, что наиболее удобными при анализе цепочек являются грамматики, допускающие детерминированный разбор, когда на каждом шаге мы можем однозначно выбрать альтернативу, и в случае невозможности подобрать нужную альтернативу цепочка не принадлежит языку (никакой вывод не может быть построен). Одним из таких типов грамматик являются LL(k) -грамматики.

11.1 LL(k) -грамматики

LL(k) -грамматиками называются грамматики, допускающие детерминированное построение левого разбора (left) при чтении анализируемой цепочки слева (left) направо, подсмат­ривая вперед не более чем на k символов.

Например, рассмотрим грамматику с множеством правил:

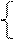S ®a S½bB

B ® b B½l

Эта грамматика является LL(1) -грамматик, т.к. для выбора правильной альтернативы на каждом шаге нам достаточно анализировать один (текущий) символ цепочки.

Грамматика называется разделённой, если все правила грамматики имеют вид

A®a₁j₁½a₂ j₂½…½a_kj_k, причём a_i¹a_j при i¹j, a_iÎV_T, j_iÎ(V_TÈV_N)* при iÎ[1,k]. Очевидно, что в случае разделённой грамматики строится детерминированный нисходящий разбор.

Очевидно, что разделённые грамматики принадлежат к классу LL(1) грамматик. Грамматики могут оказаться LL(k) грамматиками для различных k, например, грамматика может быть LL(3) грамматикой, но не LL(2) грамматикой. Бывают и грамматики, которые не являются LL(k) грамматикой ни для какого k.

Например, рассмотрим грамматику с множеством правил:

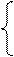S ®0 S½0B

A ® 0 A a½c L(G)= {0ⁿ⁺¹ c aⁿ, 0ⁿ⁺¹ d bⁿ, n³ 0}

B ® 0 B b½d

SÞ_l AÞ ⁿ⁺¹0ⁿ⁺¹ с aⁿ

SÞ_l BÞ ⁿ⁺¹ 0ⁿ⁺¹ d bⁿ (n ³ 0).

Чтобы определить по заданной терминальной цепочке, ка­кое правило (S ® A или S ® B) было применено на первом шаге вывода, нужно прочитать n+1 символ, следовательно данная грамматика не является LL(k) ни при ка­ком k

Дадим формальное определение LL(k) грамматики. Для этого введем определение

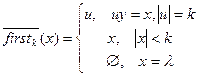
- определяются первые k символов терминальной цепочки. Т.к. для пустой цепочки это пустое множество, то определим для данной грамматики пополненную грамматику, к которой не будут встречаться пустые цепочки:

Для грамматики G=< V_T,V_N, S, R> соответствующая пополненная грамматика G’=< V_TÈ{$},V_NÈ{S’}, S’, R’>, где множество правил R’=RÈ{S’® S $ }, где каждая цепочка имеет справа граничный маркер($).

Расширим определение множества first так, чтобы охватить произвольные цепочки aÎ (V_TÈV_N) *:

Для aÎ (V_TÈV_N) * First_k(a)= { x/ aÞ* Z, ZÎ V_T *, x=}.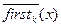

Например, рассмотрим грамматику с множеством правил

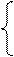S ® abA½abB

A ® ab A ½c L(G)= {(ab)ⁿc, (abc)ⁿ, n³ 1}

B ® cab B½c

Правила соответствующей пополненной грамматики:

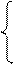S’® S $

S ® abA½abB

A ® ab A ½c

B ® cab B½c

Для данной грамматики

First₁(S)={a}, First₁(A)={a, c}, First₁(B)={c}; First₂(S)={ab}, First₂(A)={ab, c$}, First₂(B)={c$, ca}, First₃(S)={abc}, First₃(A)={abc, c$}, First₃(B)={c$, cab}.

Тогда мы можем формально определить LL(k) грамматику как грамматику, для которой для любых двух левых выводов

SÞ*w A aÞ w b a Þ *w x

SÞ*w A aÞ w g a Þ *w y

AÎV_N, w, x, y Î V_T*, a, b, g Î (V_N È V_T)*, из условияFirst_k(x)=First_k(y) следует b=g.

Несложно показать, что наше формальное определение соответствует не формальному.

Теорема: LL(k) грамматика является однозначной.

Неоднозначность грамматики противоречит LL(k) свойству. Неоднозначна – значит, существуют два вывода для некоторой цепочки, значит, не сможем определить по k символам, каое из правил следует применить.

Теорема: КС-грамматика G=< V_T,V_N, S, R> является LL(k) грамматикой Û для любых двух правил А®j₁ и А®j₂ First_k(j₁ a)Ç First_k(j₂ a)=Æ для любой цепочки a, такой что SÞ*wAa.

Использование LL(k) свойства при построении анализатора.

Пусть текущее состояние левого вывода цепочки z=wy имеет вид wАa, где w выведенное терминальное начало цепочки, А – текущий нетерминал(самый левый нетерминал), y не просмотренная часть цепочки.

Рассмотрим First_k(y). Пусть для нетерминала А существуют альтернативы:

А®j₁½j₂½¼j_n ÎR. Надо найти j_i для применения на данном шаге. Для этого надо вычислить 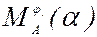=First_k(j_ia). Это множество может быть заранее вычислено для всех А, a, j_i. При этом из LL(k) свойства следует, что 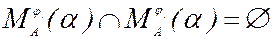при i¹j.

Выбираем j_i, такое, что First_k(y)= First_k(j_ia). Если такого j_i нет, то zÏL(G).

Затем переходим к анализу полученной цепочки xÞwyÞw’y’, где w’ – терминальное начало цепочки wj₁a.

Шаги повторяются, пока не разберём всю цепочку, или не установим, что zÏL(G).

Пример:

Рассмотрим анализ цепочки acbbd в грамматике

S ®ac S½bB

B ® b B½d

Эта грамматика является LL(1) На первом шаге определяем, какое правило применялось вначале: First₁(acS)={a}, First₁(bB)={b}, поэтому на первом шаге применяется правило S ®ac S, анализируемая цепочка принимает вид:bbd, First₁(bbd)={b}, поэтому применяется правило S ® bB, и анализируемая цепочка принимает вид bd. Определяем First₁(bB)={b}, First₁(d)={d}, поэтому применяемое правило B ® b B, анализируемая цепочка принимает вид d, применяем правило B ® d, остается пустая цепочка как в выводе, так и анализируемая цепочка, поэтому анализируемая цепочка принадлежит языку, порождаемому грамматикой.

Проблемы, возникающие при построении анализатора для LL(k) грамматик:

1. При k>1 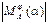может стать неприемлемо большой, т.к. 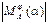пропорциональна k.

2. 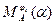является функцией от трёх переменных: А, j_i, a - т.е. велик сам объём предварительных вычислений.

Однако можно упростить задачу, усилив условия, накладываемые на грамматику:

Обозначим 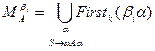и потребуем, чтобы 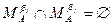при i¹j.

Грамматика G называется строго LL(k) грамматикой, если для любых двух левых выводов

SÞ*w₁ A a₁Þ w₁ b a₁Þ *w₁x

SÞ*w₂A a₂ Þ w₂ g a₂ Þ *w₂ y

AÎV_N, w₁, w₂, x, y Î V_T*, a₁, a₂, b, g Î (V_N È V_T)*, из условияFirst_k(x)=First_k(y) следует b=g. Несложно показать, что G является строго LL(k) грамматикой Û для любого AÎV_N из того, что A®bÎR, A®gÎR, b¹g, следует, что M_A^bÇM_A^g=Æ.

Теорема: LL(1) грамматика всегда строго LL(1) грамматика.

Доказательство:

Предположим, что некоторая грамматика G - LL(1) грамматика, но не строго LL(1) грамматика. Тогда существуют два вывода

SÞ*w₁ A a₁Þ w₁ b a₁Þ *w₁x₁a₁Þ *w₁x₁y₁

SÞ*w₂A a₂ Þ w₂ g a₂ Þ *w₂ x₁a₂Þ *w₁ x₂y₂,

Такие, что First₁ (x₁y₁)= First₁(x₂y₂) & b¹g - Условие (*).

Но т.к. G - LL(1) грамматика, то
SÞ*w₁ A a₁Þ w₁ b a₁Þ *w₁x₁a₁Þ *w₁x₁y₁

SÞ*w₁ A a₁Þ w₁ g a₁Þ *w₁x₂a₁Þ *w₁x₂y₁

и из First₁ (x₁y₁)= First₁(x₂y₁) следует, что b=g - Условие (**).

Покажем, что условия (*) и (**) несовместны.

Рассмотрим следующие случаи:

1. x₁¹l, x₂¹l, тогда First₁(x₁y₁)=First₁(x₁), First₁(x₂y₂)=First₁(x₂), First₁(x₁)=First₁(x₂)по условию (*) b¹g.

С другой стороны, по условию (**) First₁(x₁)=First₁(x₂)Þb=g. Противоречие.

2. x₁=l, x₂=l приводит к неоднозначности грамматики.

3. Пусть x₁=l, x₂¹l. Тогда в условии (*)First₁(x₁y₁)=First₁(y₁)= First₁(x₂y₂)=First₁(x₂) & b¹g

По условию (**) First₁(x₁y₁)=First₁(y₁)= First₁(x₂y₁)=First₁(x₂) & b=g. Противоречие.

Случай 4, x₁¹l, x₂=l разбирается аналогично случаю 3.

Из теоремы следует критерий принадлежности грамматики классу LL(1):

G – LL(1)Û M_A^bÇM_A^g=Æ при b¹g для всех AÎV_N, где M_A^b=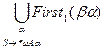

При этом если

а) "m,bÞ*m, m¹l, то M_A^b=First₁(b)

b) bÞ*l, M_A^b=First₁(b)È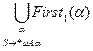

Т.К. рассматриваем пополненную грамматику, то a¹l (First₁(l)=Æ).

Определим множество Follow₁(X)={a/ SÞ⁺wXab&aÎV_T}, XÎ(V_NÈV_T).

Т.о. G - LL(1) грамматика Û "AÎV_N, "b,"g A®bÎR&A®gÎR&b¹g Þ M_A^bÇM_A^g=Æ.

Определения и алгоритмы нахождения множеств First и Follow

1. First₁(b)

1.1. First₁(l)=Æ

1.2. "aÎV_T First₁(a)=a

1.3. First₁(A)={ First₁(x_i)/A®x₁x₂…x_nÎR&i=1Úi=m&x₁…x_m-1Þ⁺l}

1.4. First₁(x₁x₂…x_n)={ First₁(x_i)/ First₁(x₁)& i=1Úi=m&x₁…x_m-1Þ⁺l}

Например, рассмотрим грамматику:

S ® ABC½CA

A®a½l

B ® b B½l

C®cC½d

В пополненной грамматике добавляется начальной правило S’® S$.

S’® S

S ® ABC½CA

A®a½l

B ® b B½l

C®cC½d

First₁(A)={a};

First₁(B)={b};

First₁(C)={c,d};

First₁(S)= First₁(ABC)È First₁(AC)={a, b, c, d}

2. Follow₁(A)= 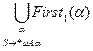={First₁(a)/ S Þ*w A a }

Рассматриваем грамматику без непроизводящих правил, тогда если S Þ*j B yÞ j d A g y, то First₁(g y)Í Follow₁(A).

2.1. Неверно, что gÞ*l, тогда First₁(gy)=First₁(g).

2.2. gÞ*l, тогда First₁(gy)=First₁(g)ÈFirst₁(y).

Поэтому Follow₁(A)={ First₁(Xm)/ B®d A X₁ X₂…X_nÎR&m=1ÚX₁X₂…X_mÞ*l}È {Follow₁(B)/B®d A g ÎR &gÞ*l}

Т.е. просматриваются все правые части правил, в которые входит исследуемый нетерминал.

Рассмотрим грамматику

S’® S $

S ® ABC½CA

A®a½l

B ® b B½l

C®cC½d

Здесь N_l={A,B}

Follow₁(S)={$},

Follow₁(A)= First₁(B)È First₁(C) È Follow₁(S)={b, c, d, $},

Follow₁(B)= First₁(C)={c,d},

Follow₁(C)= First₁(A))È Follow₁(S)={a,$}.

Проанализируем LL(1) свойство грамматики:

M_S^ABC= First₁(A)È First₁(B)È First₁(C)={a, b, c, d},

M_S^CA= First₁(C)={c,d}.

Т.к. M_S^ABC ÇM_S^CA¹Æ, то грамматика не является LL(1) –грамматикой.

Восходящий анализ.

При восходящем анализе цепочка сворачивается путем применения правил в обратном порядке (дерево вывода строится снизу вверх).

Введенные строки анализируются слева направо, полученные подстроки сопоставляются в правыми частями грамматики, и при совпадении заменяются на соответствующий нетерминальный символ в левой части правила (свёртка). Цепочка, заменяемая на этот символ, называется основой.

Если свёртываемая основа выбирается случайно, то может потребоваться возврат, и число шагов построения вывода пропорционально длине цепочки.

Среди грамматик выделяется класс LR(k) грамматик - тот тип грамматик, для которых однозначно восстанавливается правый вывод (R) при чтении цепочки слева (L) направо, при подглядывании вперёд не более чем на k символов.

Алгоритм такого разбора в общем случае сложен, поэтому чаще всего рассматривается удобный подкласс ГПП (грамматики простого предшествования) – частный случай LR(k) грамматик, в которых для выделения основы используются отношения простого предшествования.

Пусть цепочка X получена G=< V_T,V_N, S, R> с помощью правого вывода:

SÞb₁Þb₂Þ….Þb_n=X Î(V_T) *.

Тогда при восходящем анализе будем иметь

X=b_n ├ b_n-1 …├ b₀ = S.

Выделим i-ый шаг вывода SÞ*aAy (=b_i-1)Þ a j y (=b_i)Þ*x y, здесь aAy текущее состояние правого вывода, A – самый правый нетерминал в выводе. Свёртка состоит в переходе от a j y к aAy, (a j y ├ aAy) т.е. мы должны выделить подцепочку j, которая сворачивается в нетерминал A применением правила AÞ j в обратном порядке.

Пример разбора цепочки для грамматики с арифметикой.

Для ГПП техника выделения основы следующая:

Строится матрица отношений предшествования между символами V_TÈV_N. При этом между парой символов х и y может существовать не более одного отношения предшествования, обозначаемого символами <o, ≗, o>.

Грубо говоря, отношения предшествования отражают порядок появления символов в правом выводе.

Если a j y – текущее состояние цепочки, где j – основа, то

Между всеми смежными символами цепочки a, выпол­няется отношение <o или ≗.

2. Между последним символом цепочки a и первым символом цепочки j (основы) выполняется отношение <o.

3. Между смежными символами основы выполняются отношения ≗.

4. Между последним символом основы и первым символом цепочки у выполняется отношение o>.

Если такое свойство отношений имеет место и для каждой пары символов определено не более одного отношения, то осно­ву легко выделить, просматривая цепочку a j y слева направо до тех пор, пока впервые не встретится отношение o>. Для нахождения левого конца основы надо возвращаться назад, пока впервые не встретится отношение <o. Цепочка, заключенная между <o и o> и будет основой. Если в грамматике нет правил с одинаковыми правыми частями, то однозначно находится нетер­минал А такой, что A ® j, что позволяет свернуть основу, полу­чая цепочку b_i-1.

Этот процесс продолжается до тех пор, пока цепочка либо не свернется к начальному символу S, либо дальнейшие свертки окажутся невозможными.

Отношения простого предшествования с указанными свойствами могут быть определены на V_NÈV_T следующим образом [1]:

X <o Y, если в R есть правило A® a X B b, и при этомBÞ⁺Yw;

X ≗ Y, если в R есть правило A® a X Y b.

Отношение o> определяется на (V_NÈV_T) ´ V_T, так как непосредственно справа от основы может быть только терминальный символ.

X o > a, если в R есть правило A® a X Y b, и B Þ⁺ g X, YÞ* a d. Так как основа может совпадать с правым или левым кон­цом цепочки, то удобно заключить анализируемую цепочку в концевые маркеры $ и $, положив для XÎ V_NÈV_T, X o > $ для всех X, для которых S Þ⁺ a X и X<o $ для всех X, для которых S Þ⁺ X a.

Грамматика G называется грамматикой простого предшествования, если она не содержит l -правил, для любой пары символов из V_NÈV_T выполняется не более одного отношения простого предшествования и в ней нет правил с одинаковыми правыми частями.

Выполнение этих требований, очевидно, гарантирует возможность на любом шаге разбора однозначно выделить основу и произвести свертку.

Пример. Пусть множество правилграмматики: S® a S S b, S® c. Для заключения цепочки в маркеры вводим новый начальный символ S’ и правило S’®$S$. Отношения предшествования для этой грамматики приведены в табл.1.

	S	a	b	c	$
S	≗	<o	≗	<o
a	≗	<o		<o
b		o>	o>	o>	o>
c		o>	o>	o>	o>
$		<o		<o

Разбор цепочки $accb$.$< o a< o c o> cb$├$< o a ≗ S< o c o> b$├$< o a ≗ S ≗ S ≗ b o> $├$S$

Вывод, соответствующий этому разбору:

S’Þ $ S $Þ$ a S S b $Þ$ a S c b $Þ$ a c c b $
Способ построения свёртки для цепочки связан с использованием стека, куда посимвольно переносится информация из входного буфера, до тех пор, пока не встретится отношение o>. Тогда к цепочке от отношения o> до ближайшего слева отношения < o должна применяться свёртка.

Алгоритм разбора для ГПП:

1. Анализируемая цепочка заключается в маркеры.

2. Берём очередной символ из входного буфера (слева направо). Если между верхним символом стека и первым символом входной цепочки отношение< o или ≗, то заносим этот символ из входной цепочки в стек и возвращаемся к шагу 2, если же между верхним символом стека и первым символом входной цепочки отношение o>, то переходим к шагу 3. Если между символами нет никакого отношения предшествования, то цепочка не принадлежит языку, порождаемому грамматикой.

3. Обратное движение: из стека вынимаются символы до первого отношения < o между первым символом стека и символом цепочки во входном буфере. Если такой символ появился, то переходим к шагу 4, иначе цепочка не принадлежит языку, порождаемому грамматикой.

4. Применяем свёртку (заменяем выделенный фрагмент на левую часть правила грамматики, правая часть которого совпадает с основой) и возвращаемся к шагу 2. Если свёртка неприменима (нет такой правой части правила), то цепочка не принадлежит языку, порождаемому грамматикой.

Если в результате применения свёртки мы приходим к цепочке $ S $, то исходная цепочка принадлежит языку, порождаемому грамматикой, в противном случае цепочка не принадлежит языку, порождаемому грамматикой.

Обозначим

Head(A)={X/AÞ⁺Xa} (First1(A)=Head(A)ÇV_T),

Tail(A)= {X/AÞ⁺ a X}, тогда

X <o Y Û A®a X B b & YÎ Head(B)

X o > a Û A®a B C b & XÎ Tail(B) & aÎFirst1(C).

Пример разбора цепочки aaccbbcb с использованием построенной таблицы отношений предшествования приведен в табл.2.

Таблица 2

	Отношение	Входная
Стек	предшествования	строка	Операция
$	<o	aaccbcb$	сдвиг
$a	<o	accbcb$	сдвиг
$aa	<o	ccbcb$	сдвиг
$aac	o>	cbcb$	«Свертка»
$aaS	<o	cbcb$	сдвиг
$aaSc	o>	bcb$	«Свертка»
$aaSS	≗	bcb$	сдвиг
$aaSSb	o>	cb$	«Свертка»
$aS	<o	cb$	сдвиг
$aSc	o>	b$	«Свертка»
$aSS	≗	b$	сдвиг
$aSSb	o>	$	«Свертка»
$S		$	«Конец»

12.Элементы теории конечных автоматов

Конечный автомат (автомат Мили) S=< V_a, Q, V_b, q₀, F, G>, где

V_a={a₁,a₂,…a_m}, m³1 – входной алфавит автомата,

V_b= {b₁, b₂, …, b_n}, n³1 – выходной алфавит автомата,

Q= {q₀,q₁,…q_k}, k³0 – внутренний алфавит (алфавит состояний),

q₀ÎQ – начальное состояние автомата,

F - функция переходов; F: Q´ V_a ®Q,

G - функция выходов, G: Q´ V_a ® V_b.

Автомат однозначно задает отображение V_a* ® V_b* (входной цепочки в выходную).

Модель автомата – абстрактное устройство с входной и выходной лентами и управляющей головкой.

В каждый момент времени автомат находится в одном из состояний множества Q, воспринимает один из символов входного алфавита (содержащийся в ячейке, с которой происходит считывание), и печатает один символ выходного алфавита на выходной ленте. Время у нас считается дискретным.

Существуют две традиции в задании автоматов. Первая из них - явное задание дискретного времени, т.е. номера такта tÎN(= {0,1,2,…}, a(t)ÎV_a, b(t) ÎV_b, q(t) ÎQ.

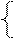Тогда работа автомата описывается с помощью рекуррентных соотношений:

q(t+1)=f (q(t),a(t))

b(t)=g(q(t),a(t))

Иногда рассматривается b(t+1)=g(q(t),a(t)) – автомат с задержкой; мы такие автоматы не рассматриваем, т.к. это для некоторых задач неудобно.

Граф переходов автомата определяется следующим образом:

Множество вершин графа – каждая вершина соответствует элементу множества Q, множество ребер определяется отображениями F и G, причём F определяет связи (переходы состояний), а G – выходы. Отображения в общем случае частичные, но если определено f(q_i,a_j), то определено и g(q_i,a_j).

Пример. Пусть граф переходов автомата представлен на рис.26.

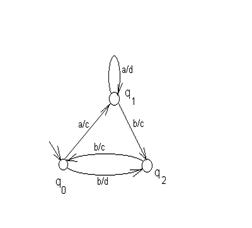
Рис. 26. Пример автомата Мили.

При входной цепочке aabb получается выходная цепочка cdcc.

Функции переходов и выходов определяют автоматное отображение V_a*®V_b*. При этом для любой входной цепочки a=a₁a₂….a_k f(q₀, a₁a₂….a_k)= f(f(…f(q₀, a₁)a₂)…. a_k)

Или, эквивалентное индуктивное определение:

1. f(q_i, a_j) определяется по таблице перехода автомата,

2. f(q_i, a a_j)= f (f(q_i, a), a_j).

Соответствующая функция выхода:

1. g(q_i, a_j) определяется по таблице перехода автомата,

2. g(q_i, a a_j)= g (f(q_i, a), a_j).

Тогда входному слову a=a₁a₂….a_k ставится в соответствие выходное слово w(a)=g(q₀,a₁)g(q₀,a₁ a₂), …g (q₀, a₁a₂….a_k).

Это отображение, ставящее в соответствие входным словам выходные слова, называется автоматным отображение, или автоматным оператором, реализуемым автоматом S. Будем говорить, что S(a)=w.

Автоматное отображение можно определить индуктивно, как и функцию переходов.

1. S(q₀, a_j)= g(q₀, a_j)

2. S(q_i, a a_j)= S(q0, a)g (q₀, a), a_j).

Как и ранее, длина цепочки a обозначается½a½.

Свойства автоматного отображения:

1. a и w = S(a) имеют одинаковую длину ½a½=½ S(a)½.

2. Если a=a₁a₂, и S(a₁a₂)=w₁w₂, где ½a₁½=½w₁½, то S(a₁)= w₁.

Т.е. автоматный оператор является оператором без «предвосхищения», без заглядывания вперед, например, мы не можем построить инверсию слова.

Говорят, что состояние q_j достижимо из состояния q_i, если $aÎ V_a*, такая, что f(q_i, a)=q_j.

Автомат S называется сильно связным, если любое состояние достижимо из любого другого.

Два автомата S и T изоморфны, если входы, выходы и состояния автомата S можно переименовать таким образом, чтобы таблица переходов автомата S превратилась в таблицу переходов автомата Т.

Например, автомат на рис. 26 изоморфен автомату на рис. 27. Если же заменить f на c на стрелке из q_C в q_A, то автоматы становятся неэквивалентны.

Соответствия:

a – b, b – a

c – c, d – f

q₀ – q_A

q₁ – q_B

q₂ - q_C

Рис.27. Автомат Мили, изоморфный автомату на рис. 26.

Пусть T и S автоматы с одинаковыми входными и выходными алфавитами. Состояние q автомата S и состояние r автомата T называются неразличимыми, если для любой входной цепочки aÎVa* S(q,a)=T(r,a). При T=S говорим о неразличимых состояниях одного автомата.

Если неразличимы входные состояния двух автоматов, то они реализуют одно и то же автоматное отображение. В этом случае автоматы эквивалентны.

Переход от автомата к эквивалентному – эквивалентное преобразование автомата.

Автоматы Мура.

Отличаются от автоматов Мили тем, что здесь одному состоянию (а не переходу) соответствует один выход.

Конечный автомат Мура: S=< V_a, Q, V_b, q₀, F, G>, где

V_a={a₁,a₂,…a_m}, m³1 – входной алфавит автомата,

V_b= {b₁, b₂, …, b_n}, n³1 – выходной алфавит автомата,

Q= {q₀,q₁,…q_k}, k³0 – внутренний алфавит (алфавит состояний),

q₀ÎQ – начальное состояние автомата,

F - функция переходов; F: Q´ V_a ®Q,

G - функция выходов, G: Q ® V_b.

Приняты две схемы задания автоматов Мура:

Первая схема	Вторая схема
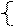q (t+1) =f (q(t), a(t)) b(t)= g(q(t))	q (t+1) =f (q(t), a(t)) b(t)= g(q(t+1))

При работе по первой схеме выход автомата однозначно соответствует состоянию, из которого совершается переход, по второй – состоянию, в которое автомат переходит. Хотя при записи уравнений первая схема выглядит более естественно, условие второй схемы реализовать проще: в соответствующих автоматах Мили для первой схемы должны быть одинаковые выходы на всех дугах, выходящих из состояния, для второй – одинаковые выходы должны быть на дугах, ведущих в состояние.

Рассмотрим автомат Мура, представленный на рис. 28

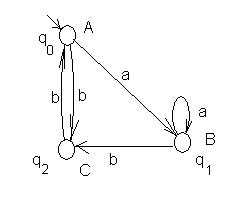
Рис.28 Автомат Мура

Здесь выходы, соответствующие состояниям, изображены справа от состояния. Если рассматривать работу автомата по первой схеме, то входу aabb будет соответствовать выход ABBC, если же по строй схеме, то этому же входу соответствует выход BBCA.

По автомату Мура всегда можно построить автомат Мили.

Автомат Мили, эквивалентный автомату Мура, представленному на рис. 28, при работе по первой схеме, дан на рис. 29, а при работе по второй схеме – на рис.30.

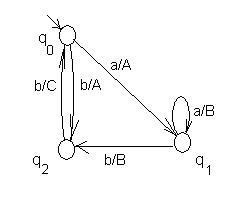
Рис. 29. Автомат Мили, эквивалентный автомату Мура на рис. 28, при работе по 1-ой схеме, здесь все дуги, ведущие из состояния, имеют одинаковые выходы.

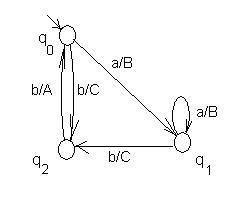
Рис.30. Автомат Мили, эквивалентный автомату Мура на рис. 28, при работе по 2-ой схеме, здесь все дуги, ведущие в состояние, имеют одинаковые выходы.

По выразительной мощности эти модели (автоматы Мили и Мура) эквивалентны, если используется вторая версия для представления автоматов Мура. (Очевидно, что по автомату Мура всегда можно построить автомат Мили.)

Построение автомата Мура (вторая схема) по автомату Мили:

а) Если все дуги, ведущие в некоторое состояние q_k, имеют одинаковые выходные пометки b_s, то эта пометка просто переносится на это состояние (рис.31).

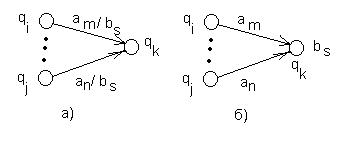
Рис. 31

Формально это условие для состояния q_k и выхода b_s можно записать так:

"q_i,q_j,an,a_m (f(q_i,a_n)= f(q_j,a_m)= q_k Þ g(q_i,a_n)= g(q_j,a_m)= b_s)

б) Общий случай: в некоторые вершины ведут дуги, помеченные разными символами. В этом случае все q_k такие вершины расщепляются на множество вершин (расщепление состояния), помечаемых символами <q_k,b_j> (рис.32).

q_k®{<q_k, b_s>/ f(q_i, a)=q_k, g(q_i, a)=b_s}

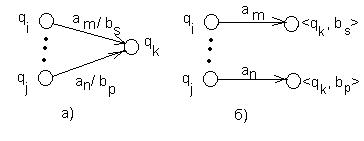
Рис. 32. Расщепление вершины.

В общем случае число состояний увеличивается. Затем для каждого состояния q_i исходного автомата Мили и для каждой дуги из состояния q_i в состояние q_k с пометкой a_p/b_s(a_p - вход, b_s - выход) строятся дуги из всех <q_i,b_j> в <q_k, b_s> и помечаются a_p.

Кроме того, если начальное состояние q0 расщепилось, вводится новое начальное состояние, в которое не ведет ни одна дуга.

Затем приписываем состояниям соответствующие выходы и переобозначаем состояния.

Например, рассмотрим автомат Мили (Рис. 33, а), приведенный так же на рис. 26. У этого автомата состояния q₁ и q₂ расщепляются, а q₀ нет, поэтому нет необходимости вводить новое входное состояние. Полученный эквивалентный автомат Мура приведён на рис. 33.б.

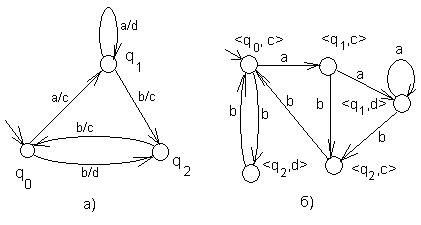
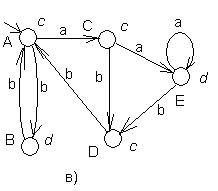
Рис. 33. Автомат Мили(а) и эквивалентный ему автомат Мура(б) до и после (в) переобозначения состояний.

Таким образом, полный алгоритм построения эквивалентного автомата Мура по автомату Мили выглядит следующим образом:

1) Расщепляем состояния.

2) Вводим дополнительное входное состояние (если входное состояние расщепилось).

3) Строим дуги, соответствующие дугам исходного автомата.

4) Переносим выходные символы на соответствующие состояния.

5) Переобозначаем состояния.

Таким образом, установлено соответствие между разными типами автоматов.

Частичные автоматы

Автомат S называется частичным автоматом, если хотя бы одна из двух функций (F или G) не полностью определена, т.е. для некоторых пар (состояние,вход) значение F или G не определено (обозначается прочерками в таблице).

Состояния A и B называются псевдоэквивалентными (обозначается A@B), если они одновременно не определены или определены и равны функции F и G. Эти функции для частичных автоматов определяются следующим образом:

f(q_i,a)

1) f(q_i, a_j) – по таблице переходов автомата

2) если f(q_i,a) определена, то f(q_i,a a_j)@f(f(q_i,a),a_j)

3) если f(q_i,a) не определена, то не определена и f(q_i,a a_j) для всех a_j.

g(q_i,a a_j)

1) g(q_i, a_j) – по таблице переходов автомата

2) g(q_i,a a_j)@g (f(q_i,a), a_j).

Автоматное отображение:

1) S(q_i, a_j)= g(q_i, a_j) (если g(q_i, a_j) не определено, то S(q_i, a_j) считаем равным прочерку)

2) если f(q_i,a) определена, то S(q_i,a a_j)=S(q_i,a) g(f(q_i,a) a_j). Если g(f(q_i,a), a_j) не определена, то считаем её равной прочерку)

3) если f(q_i,a) не определена, то не определена и S(q_i,a a_j) для всех a_j.

Входное слово a, для которого S(q_i,a) определено, называется допустимым для S.

Отметим неравноправность функций f и g – неопределенность g не препятствует допустимости слова, а неопределенность функции f для некоторого слова говорит о недопустимости любого его продолжения.

Состояния q_i Î S и r_jÎT псевдонеотличимы (псевдоэквивалентны), если для любой цепочки a S(q_i,a)@T(rj,a) (Т.е. области определённости и неопределённости для q_i и r_j совпадают, и в области определённости отображения совпадают).

Автоматы S и T псевдонеотличимы, если для любого состояния автомата S найдётся псевдонеотличимое от него состояние автомата T, а наоборот, для любого состояния автомата T найдётся псевдонеотличимое от него состояние автомата S.

Для полностью определённых автоматов псевдонеотличимость совпадает с обычной неотличимостью.

Отношение псевдонеотличимости является отношением эквивалентности.

Пример псевдоэквивалентных автоматов приведён на рис.34.

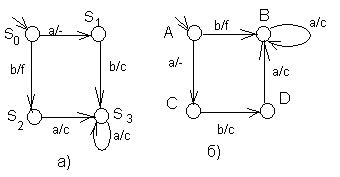
Рис.34. Пример псевдоэквивалентных автоматов. Здесь соответствия состояний

S0 – A S2 – B, D S3 – B, D S4 - C

A – S0 B – S3,S2 C – S1 D – S2,S3

Недостаток введённого определения псевдоэквивалентности – необходимость совпадения областей определения. Можно дать эквивалентное определение, не требующее анализа совпадения областей: вводим новое, дополнительное состояние, переход в которое осуществляется при отсутствии перехода по данному входу, для которого переход по любому входу осуществляется в само себя, а в функции выхода прочерк будем рассматривать как дополнительную букву, таким образом автомат становится полностью определённым.

Минимизация не полностью определённых автоматов возможна двух типов: «строгая», с сохранением областей определения (что производится просто, как для доопределённого автомата), и через покрытия состояний, когда требуется совпадение переходов только в области определённости.

Если проводить строгую минимизацию, то автомат на рис. 34 а минимизируется до автомата, граф переходов которого приведен на рис. 35.

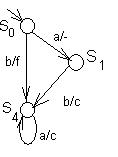
Рис. 35. Минимизированный автомат.

Два основных аспекта работы автомата:

1. Автоматы распознают входные слова, т.е. отвечают на вопрос aÎМ? (распознаватели)

2. Преобразуют входные слова в выходные(автоматные отображения):

с одной стороны, последовательность ответов распознавателя на входные слова а₁, а₁а₂, … образуют выходное слово, которое является автоматным отображением;

с другой стороны, выходные буквы можно разбить на два класса С₁ и С₂, и считаем, что слово распознаётся, если g(q_i,a)Î С₁. Таким образом, эти два представления автоматов являются эквивалентными.

Интерпретация автоматов: Дискретное устройство, входная буква – входной сигнал, выходное слово – последовательность сигналов.

Свойство автоматов:

Теорема:

Существуют события, не представимые в конечных автоматах: никакая непериодическая последовательность не распознаваема в конечных автоматах(например, 010110111011110111110…)

Док-во:

Пусть непериодическая последовательность a=a₁a₂…a_j… распознаётся автоматом S с n состояниями. Тогда для любого начального отрезка a₁a₂…a_j f(a₁a₂…a_j)= q_kÎ C₁. но тогда проходится последовательность состояний из C₁, а оно конечно, значит, некоторое состояние встретится дважды: q_s=q_s+p. Значит, f(q_s, a_s+1…a_s+p)=q_s, поэтому периодическая последовательность так же будет распознаваться автоматом, и, следовательно, непериодическая последовательность не может распознаваться конечным автоматом вопреки предположению.