Автомат (Мили) называется комбинационным, если для любого входного символа a и любых состояний qi и qj g(qi,a)=g(qj,a), иначе говоря, если выходной симовл не зависит от текущего состояния и определяется входным символом (все состояния автомата в данном случае эквивалентны, т.е. минимизированный автомат будет иметь всего одно состояние).
Автомат называется логическим, если его входной алфавит состоит из 2m двоичных наборов длины m, а выходной алфавит – 2n двоичных наборов длины n. Тогда функция выхода – набор из n логических функций от m переменных. Можно получать автоматные блок-схемы, например, схему, представленную на рис. 36.
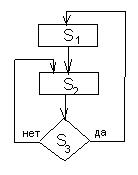
Рис. 36. Схема автоматов.
Следует отметить, что автоматы в такой схеме должны уметь останавливаться.
Возможны различные случаи рассмотрения автоматных схем.
1. Если алфавиты автоматов не пересекаются. В этом случае действуют обычные правила минимизации для частичных автоматов, и для правильных последовательностей входных сигналов число суммарное состояний получаемого автомата – max ½Qi½.
2. Если входные алфавиты исходных автоматов совпадают или включают друг друга, тогда множество состояний является объединением множества состояний исходных состояний, затем могут производиться эквивалентные преобразования автомата, в этом случае число состояний £ S ½Qi½.
В любом случае блок-схема автоматов, работающих последовательно – конечный автомат S, значит, множество автоматов замкнуто относительно операции условного и безусловного перехода(следовательно, каждая программа является автоматом, и каждый алгоритм так же).
Синхронные сети автоматов.
Поскольку автомат – устройство с входом и выходом, то присоединение к входам одного автоматов выходов другого образует сеть, или схему, автоматов.
Под состоянием сети из m автоматов S1, S2,…,Sm понимается вектор (qi1,,,,qim), где каждое qij состояние автомата j. В общем случае число состояний автомата, полученного в результате построения сети – произведение числа состояний исходных автоматов.
Является ли полученная схема автоматом?
Один из способов введения времени – синхронный: такты, границы тактов нумеруются натуральными числами, начиная с 0.
Длина такта рассматривается как единица времени. Входное слово – временная последовательность сигналов (импульсов). Интервал между соседними импульсами – длина такта. Слово длины k будет обрабатываться за k тактов. Входная информация - a(t).
Автоматные функции f и g реализуются с задержкой; f (q(t), a(t))=q(t+1), q(0) –задаётся отдельно,
g(q(t),a(t))=b(t) обычно, (иногда g(q(t),a(t))= b(t+1), тогда задаётся b(0))
Виды соединения автоматов:
a) С разделительными входами и алфавитами А1 и А2 (рис. 37.а). S =<A, Q,V, q0, F,G>
В этом случае входной алфавит A= А1´А2, внутренний алфавит Q= Q1´Q2, выходной алфавит V= V1´V2. S называется прямым произведением автоматов S1 и S2. В этом случае a=(a1,a2) (Здесь верхний индекс означает отнесение к соответствующему алфавиту).
f((q1,q2), (a1,a2))=(f1(q1,a1),f2(q2,a2)).
Мы рассмотрели случай, когда два входа и два выхода. Может быть произвольное число входов и выходов.
b) С общим входом и алфавитом А (рис. 37 б).
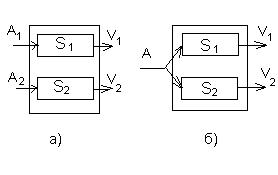
В этом случае f((q1,q2), a)=(f1(q1,a),f2(q2,a)). Определение выходов в обоих случаях очевидно.
Рис. 37 Параллельное соединение автоматов.
2) Последовательное соединение автоматов (рис.38).

S =<A, Q,V, q0, F,G>, A=A1, V=V2, V1=A2, Q= Q1´Q2. Для F и G существенна задержка g1. Если задержка g1 равна 0, т.е. g1(q1(t), a(t))=v1(t), то q(t+1)=(q1(t+1),q2(t+1))= (f1(q1(t),a(t)), f2(q2(t), g1 (q1(t),a(t))), т.е. зависимость существует только от q(t), a(t), при этом состояние q(t+1)=f(q(t),a(t)), выход g((q1,q2),a)=g2(q2,g1(q1,a)).
Если же задержка g1 равна 1, т.е. g1(q1(t), a(t))=v1(t+1), то q(t+1= (f1(q1(t),a(t)), f2(q2(t), g1 (q1(t-1),a(t-1))), и такой простой зависимости, как для прошлого случая, нет.
Пример.
рассмотрим схему из двух элементов задержки, воспроизводящих вход через 1 такт. S1 и S2 имеют по одному состоянию, начальное значение выхода =0, S(a)=00a-2 (отбрасываются два последних символа последовательности).
Таблица переходов автомата, реализующего задержку:
| q0 | q1 | |
| q0, 0 | q1, 1 | |
| q0, 0 | q1, 1 |
Считаем, что если задержка g равна 0, g(q(t),a(t))= v(t)=g(t)
Обозначим состояние (qi,qj) через i j. Тогда таблица переходов/выходов результирующего автомата
| 00,0 | 00,1 | 01,0 | 01,1 | |
| 10,0 | 10,1 | 11,0 | 11,1 |
Т.о. цепь из двух элементов задержки описывается автоматом без задержки.
3) Соединение автоматов с обратной связью. Общая схема представлена на рис. 39
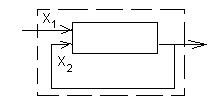
Рис.39 Схема соединения с обратной связью
Если рассматривать вариант обратной связи без задержки, то могут возникать противоречия.
Например, если s(x) функция Шеффера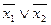 , и v(t)=0, тогда x2=0, значит, v(t)=1, а при x1=1 это даёт v(t)=0. Противоречие, т.е. в реальности состояние будет не определено.
, и v(t)=0, тогда x2=0, значит, v(t)=1, а при x1=1 это даёт v(t)=0. Противоречие, т.е. в реальности состояние будет не определено.
Поэтому вводится задержка и схема автомата приобретает следующий вид (рис.40).
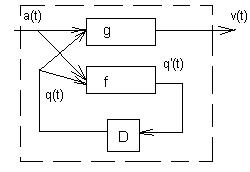
Рис.40 Общая схема автомата с обратной связью
Всякий автомат при синхронной интерпретации может быть реализован как сеть, составленная из комбинационных автоматов и элементов задержки.
На рис. 40 приведена схема для автомата с функциями
q(t+1)=f(q(t),a(t))
v(t)=g(q(t),a(t))
На рисунке g – комбинационный автомат с входным алфавитом A´Q и выходным алфавитом V, f – комбинационный автомат с входным алфавитом A´Q и выходным алфавитом Q, D – блок задержки (на 1 такт).
D – автомат Мура, входной и выходной алфавит которого Q= {q1,q2,…,qn}, множество состояний - R={r1,r2,…,rn}, ½R½=½Q½, функции g(ri)=qi, fD(ri,qj)=rj.
Частный случай D – двоичный элемент задержки, когда g1(t)=f(q(t), a(t))= q(t+1).
В важном частном случае, когда A,V,Q состоят из двоичных наборов, f и g – логические комбинационные автоматы, двоичные входы которых в момент t являются логическими функциями от двоичных переменных, образующих наборы a(t) и q(t), D – параллельное соединение элементов задержки. Число элементов задержки равно длине вектора Q, а число состояний D равно мощности входного алфавита ½Q½= 2n.
Так как произвольные конечные алфавиты могут быть закодированы двоичными наборами, то получается
Теорема. Любой конечный автомат при любом двоичном кодировании может быть реализован синхронной сетью из логических комбинационных автоматов и двоичных задержек, причем число задержек не может быть меньше log2½Q½.
Сеть из логических блоков и элементов задержки будем называть правильно построенной логической сетью (ППЛС), если
1. К каждому входу блока сети присоединён не более чем один выход блока сети (однако допускается присоединение выхода более чем к одному входу, т.е. допускается разветвление выходов)
2. В каждом контуре обратной связи, т.е. в каждом цикле, образованном блоками и соединениями между ними, имеется не менее одного элемента задержки.
Входами такой сети называются те входы блоков, к которым не присоединены никакие выходы, выходами сети называются те выходы блоков, которые не присоединены ни к каким входам (рис.41).
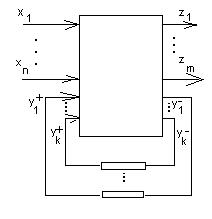
Рис. 41
Основные этапы проектирования автоматов
Mx - множество входных векторов,
Mz – множество выходных векторов,
My- - множество векторов, характеризующих входные каналы обратной связи (памяти),
My+ - множество векторов, характеризующих выходные каналы обратной связи (памяти).
Каждый из каналов в случае k-значной логики может находиться в одном из k значений из множества {0, 1,…,k-1}.
Правила вывода в грамматике, соответствующей автомату, можно определить как подстановку
XY+® Z Y-, Y+(t=0)=Y0+, Y+(t+t)=Y-(t).
Состояния каналов обратной связи будем называть внутренними состояниями автомата, а t- временем перехода из одного состояния в другое, причём t может быть постоянной для данного автомата или эже зависеть от изменения X. В первом случае автомат называется синхронным, во втором – асинхронным.
При заданном значении Y0+ последовательность входных векторов X (входная последовательность) однозначно определяет последовательность векторов Z (выходную последовательность).
Объём памяти автомата (число внутренних состояний автомата) обычно гораздо меньше объема памяти операционного автомата.
Общая структура автомата представлена на рис.42.
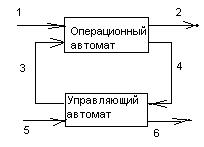
рис. 42. Общая схема автомата. Здесь
1 – преобразуемая информация,
2 – результат преобразования,
3 - управляющее воздействие, соответствующее реализуемому алгоритму,
4 - признаки, характеризующие результат
5 – сигнал, определяющий выполняемое преобразование и его начало,
6 – сигнал окончания операции.
!-2 – информационные каналы,
3-6- управляющие.
По Глушкову – ЭВМ – преобразователь информации, который целесообразно рассматривать как композицию пар автоматов (операционный+управляющий).
Общий порядок проектирования автоматов:
системное проектирование – логическое проектирование (логические блоки) – техническое проектирование.
Литература
1) Сергиевский Г.М. «Лингвистические модели», М., 1983
2) В.Дж.Рейуорд-Смит «Теория формальных языков», М., Радио и связь, 1988
3) О.П.Кузнецов, Г.М. Адельсон-Вельский «Дискретная математика для инженера», Энергоатомиздат, 1988
4) В.А. Горбатов «Основы дискретной математики», М., ВШ, 1986
5) В.А. Горбатов «Фундаментальные основы дискретной математики», М., Наука, 2000.
 2014-02-02
2014-02-02 2861
2861








