Оценку погрешности результата измерения выполняют при разработке МВИ. Источниками погрешностей являются модель ОИ, метод измерения, СИ, оператор, вляющие факторы условий измерений, алгоритм обработки результатов наблюдений. Как правило, погрешность результата измерения оценивается при доверительной вероятности Р = 0,95.
При выборе значения Р необходимо учитывать степень важности (ответственности) результата измерений. Например, если ошибка в измерении может привести к гибели людей или к тяжелым экологическим последствиям, значение Р должно быть увеличено.
1. Измерения с однократными наблюдениями. За результат измерения в этом случае принимают результат однократного наблюдения х (с введением поправки, если она имеется), используя предварительно полученные (например, при разработке МВИ) данные об источниках, составляющих погрешность.
Доверительные границы НСП результата измерения Q(P)вычисляют по формуле
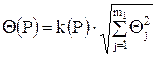 , (7)
, (7)
где k(P) - коэффициент, определяемый принятой Р и числом m 1 составляющих НСП: Q(P)- найденные нестатистическими методами границы
j -ой составляющей НСП (границы интервала, внутри которого находится эта составляющая, определяемые при отсутствии сведений о вероятности ее нахождения в этом интервале). При Р = 0,90 и 0,95 k(P) равен 0,95 и 1,1, соответственно при любом числе слагаемых m 1. При Р = 0,99 значения k(P) следующие (табл. 3):
Таблица 3
| m1 | k(P) | m1 | k(P) |
| 5 и более | 1,45 | 1,30 | |
| 1,40 | 1,20 |
Если составляющие НСП распределены равномерно и заданы доверительными границами Q(P),то доверительную границу НСП результата измерения вычисляют по формуле
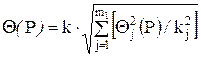 , (8)
, (8)
где k и kj - те же, что и в предыдущем случае, коэффициенты, соответствующие доверительной вероятности Р и Рj соответственно; m1 - число составляющих НСП.
Среднее квадратическое отклонение (СКО) результата измерения с однократным наблюдением вычисляют одним из следующих способов:
1. Если в технической документации на СИ или в МВИ указаны нормально распределенные составляющие случайной погрешности результата наблюдения (инструментальная, методическая, из-за влияющих факторов, оператора и т.д.), то СКО вычисляют по формуле

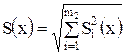 ,
,
где m2 - число составляющих случайной погрешности;
Si - значения СКО этих составляющих.
Доверительную границу случайной погрешности результата измерения Î(Р) в этом случае вычисляют по формуле
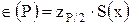 , (9)
, (9)
где zP/2 - значение нормированной функции Лапласа в точке Р/2 при доверительной вероятности Р (табл. 4):
 2014-02-02
2014-02-02 447
447








