Таблица 4
| Р | zP/2 | Р | zP/2 |
| 0,90 | 1,65 | 0,97 | 2,17 |
| 0,95 | 1,96 | 0,98 | 2,33 |
| 0,96 | 2,06 | 0,99 | 2,58 |
2. Если в тех же документах случайные составляющие погрешности результата наблюдения представлены доверительными границами Îi(P) при одной и той же доверительной вероятности P, то доверительную границу случайной погрешности результата измерения с однократным наблюдением при доверительной вероятности вычисляют по формуле
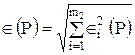 .
.
3. Если случайные составляющие погрешности результата наблюдения определяют предварительно в реальных рабочих условиях экспериментальными методами при числе наблюдений ni <30, то:
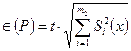 ,
,
где t - коэффициент Стьюдента, соответствующий наименьшему числу наблюдений n min из всех ni, можно найти в любом справочнике по теории вероятностей; S(x) - оценки СКО случайных составляющих погрешности результата наблюдения, определяемых по формуле (14). Если в эксперименте невозможно или нецелесообразно определить СКО составляющих случайной погрешности и определено сразу суммарное СКО, то в формуле (1.9) m2 = 1.
4. Если случайные составляющие погрешности результата наблюдений представлены доверительными границами Î(Pi), соответствующими разным вероятностям Р i, то сначала определяют СКО результата измерения с однократным наблюдением по формуле
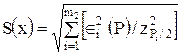 ,
,
где zPi/2 - значения функции Лапласа. Затем вычисляют Î(P) по формуле (8).
Для суммирования систематической и случайной составляющих погрешностей рекомендуется следующий способ:
Если Q(P)/S(x) < 0,8, (10)
то НСП Q(P) пренебрегают и окончательно принимают Î(P) за погрешность результата измерения D(P) при доверительной вероятности Р.
Если Q(P)/S(x) > 0,8, (11)
то пренебрегают случайной погрешностью и принимают D(P) = Q(P).
Если 0,8 £ Q(P)/S(x) £ 8, то доверительную границу погрешности результата измерений вычисляют по формуле
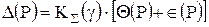 , (12)
, (12)
где KS(g) = 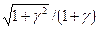 ;
; 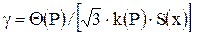 .
.
2. Измерения с многократными наблюдениями. Обработку результатов в этом случае рекомендуется начать с проверки на отсутствие промахов (грубых погрешностей). Промах — это результат xп отдельного наблюдения, входящего в ряд из n наблюдений, который для данных условий измерений резко отличается от остальных результатов этого ряда. Если оператор в ходе измерения обнаруживает такой результат и достоверно находит его причину, он вправе его отбросить и провести (при необходимости) дополнительное наблюдение взамен отброшенного.
При обработке уже имеющихся результатов наблюдений произвольно отбрасывать отдельные результаты нельзя, так как это может привести к фиктивному повышению точности результата измерения. Поэтому применяют следующую процедуру. Вычисляют среднее арифметическое 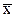 результатов наблюдений хi по формуле
результатов наблюдений хi по формуле
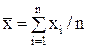 . (13)
. (13)
Затем вычисляют оценку СКО результата наблюдения как
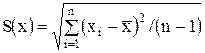 . (14)
. (14)
Находят отклонение vп предполагаемого промаха xп от 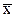 :
:
vп = | xп - 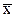 |.
|.
По числу всех наблюдений n (включая xп) и принятому для измерения значению Р (обычно 0,95) в любом справочнике по теории вероятностей находят z(P,n) — нормированное выборочное отклонение нормального распределения. Если v п < z×S(x), то наблюдение xп не является промахом; если v п ³ z×S(x), то xп — промах, подлежащий исключению. После исключения xп повторяют процедуру определения 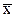 и S(x) для оставшегося ряда результатов наблюдений и проверки на промах наибольшего из оставшегося ряда отклонений от нового значениям (вычисленного исходя из n - 1).
и S(x) для оставшегося ряда результатов наблюдений и проверки на промах наибольшего из оставшегося ряда отклонений от нового значениям (вычисленного исходя из n - 1).
За результат измерения принимают среднее арифметическое 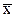 [см. формулу (13)] результатов наблюдений хi. Погрешность
[см. формулу (13)] результатов наблюдений хi. Погрешность 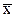 содержит случайную и систематическую составляющие. Случайную составляющую, характеризуемую СКО результата измерения, оценивают по формуле
содержит случайную и систематическую составляющие. Случайную составляющую, характеризуемую СКО результата измерения, оценивают по формуле
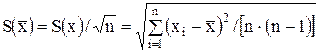 .
.
В предположении принадлежности результатов наблюдений хi к нормальному распределению находят доверительные границы случайной погрешности результата измерения при доверительной вероятности Р по формуле Î(P) = t(P,n) × S(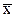 ), (15)
), (15)
где t - коэффициент Стьюдента.
Доверительные границы Q(Р) НСП результата измерения с многократными наблюдениями определяют точно так же, как и при измерении с однократным наблюдением — по формулам (1.7) или (1.8).
Суммирование систематической и случайной составляющих погрешности результата измерения при вычислении D(Р) рекомендуется осуществлять с использованием критериев и формул (10 – 12), в которых при этом S(x) заменяется на S(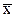 ) = S(x)/
) = S(x)/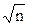 .
.
3. Косвенные измерения. Значение измеряемой величины А находят по результатам измерений аргументов а1,..., аi,…am, связанных с искомой величиной уравнением
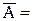 f(a1,….ai….am). (16)
f(a1,….ai….am). (16)
Вид функции f определяется при установлении модели ОИ.
Косвенное измерение при линейной зависимости. Искомая величина А связана с m измеряемыми аргументами уравнением
 ,
,
где bi - постоянные коэффициенты.
Предполагается, что корреляция между погрешностями измерений ai отсутствует. Результат измерения А вычисляют по формуле
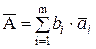 ,
,
где  — результат измерения ai с введенными поправками. Оценку СКО результата измерения S(A) вычисляют но формуле
— результат измерения ai с введенными поправками. Оценку СКО результата измерения S(A) вычисляют но формуле
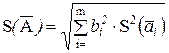 ,
,
где 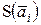 — оценка СКО результата измерений
— оценка СКО результата измерений  .
.
Доверительные границы Î(Р) случайной погрешности 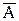 при нормальном распределении погрешностей
при нормальном распределении погрешностей 
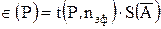 , (17)
, (17)
где t(P,nэф) — коэффициент Стьюдента, соответствующий доверительной вероятности Р (обычно 0,95, в исключительных случаях 0,99) и эффективному числу наблюдений nэф, вычисляемому по формуле
 ,
,
где ni —число наблюдений при измерении аi.
Доверительные границы Q(Р) НСП результата такого измерения, сумму Q(Р) и Î(Р) для получения окончательного значения D(Р) рекомендуется вычислять с использованием критериев и формул (7), (8), (10) — (12), в которых m1, Qi, и S(x) заменяются, соответственно, на m, bi ×Qi, и S(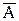 ).
).
Косвенные измерения при нелинейной зависимости. При некоррелированных погрешностях измерений аi используется метод линеаризации путем разложения функции f(а1,..., am) в ряд Тейлора, то есть
f(а1,..., am) =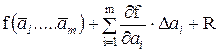 ,
,
где 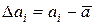 — отклонение отдельного результата наблюдения аi от
— отклонение отдельного результата наблюдения аi от 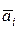 ; R — остаточный член.
; R — остаточный член.
Метод линеаризации допустим, если приращение функции f можно заменить ее полным дифференциалом. Остаточным членом
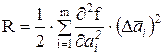 пренебрегают, если
пренебрегают, если 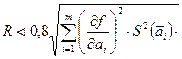 ,
,
где 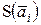 — оценка СКО случайных погрешностей результата измерения
— оценка СКО случайных погрешностей результата измерения  . При этом отклонения D
. При этом отклонения D должны быть взяты из возможных значений погрешностей и такими, чтобы они максимизировали R.
должны быть взяты из возможных значений погрешностей и такими, чтобы они максимизировали R.
Результат измерения 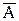 вычисляют по формуле
вычисляют по формуле 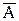 = f(
= f(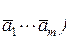 .
.
Оценку СКО случайной составляющей погрешности результата такого косвенного измерения S(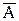 ) вычисляют по формуле
) вычисляют по формуле
 ,
,
а Î(Р) — по формуле (17). Значение nэф , границы НСП Q(Р) и погрешность D(Р) результата косвенного измерения при нелинейной зависимости вычисляют так же, как и при линейной зависимости, но с заменой коэффициентов bi на ¶f/¶ ai
Метод приведения (для косвенных измерений с нелинейной зависимостью) применяется при неизвестных распределениях погрешностей измерений ai и при корреляции между погрешностями ai для получения результата косвенного измерения и определения его погрешности. При этом предполагается наличие ряда n результатов наблюдений aij измеряемых аргументов аi. Сочетания aij, полученных в j-м эксперименте подставляют в формулу (1.16) и вычисляют ряд значений Aj измеряемой величины А. Результат измерения 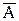 вычисляют по формуле
вычисляют по формуле 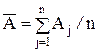 .
.
Оценку СКО S(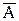 ) - случайной составляющей погрешности
) - случайной составляющей погрешности 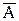 -вычисляют по формуле
-вычисляют по формуле
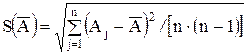 ,
,
а Î(Р) — по формуле (15). Границы НСП Q(Р) и погрешность D(Р) результата измерения 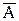 определяют описанными выше способами для нелинейной зависимости.
определяют описанными выше способами для нелинейной зависимости.
 2014-02-02
2014-02-02 543
543








