Пусть из генеральной совокупности извлечена выборка, причем 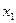 наблюдалось
наблюдалось 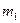 раз,
раз, 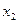 –
– 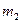 раз, …,
раз, …, 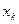 –
–  раз, при этом
раз, при этом 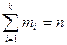 – объем выборки. Наблюдаемые значения
– объем выборки. Наблюдаемые значения 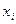 называют вариантами, а последовательность вариант, записанных в возрастающем порядке, – вариационным рядом. Числа наблюдений
называют вариантами, а последовательность вариант, записанных в возрастающем порядке, – вариационным рядом. Числа наблюдений 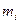 называют частотами, а их отношения к объему выборки
называют частотами, а их отношения к объему выборки  – относительными частотами.
– относительными частотами.
Для визуальной оценки распределения исследуемой выборки (СВ 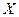 ) производят группировку данных.
) производят группировку данных.
Если изучается дискретная случайная величина, то наблюдаемые значения располагаются в порядке возрастания и подсчитываются частоты 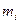 или относительные частоты
или относительные частоты 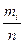 появления одинаковых значений случайной величины
появления одинаковых значений случайной величины 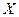 . В результате получаем сгруппированные статистические ряды следующего вида
. В результате получаем сгруппированные статистические ряды следующего вида  :
:
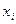 –ход эксперимента –ход эксперимента | 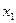 | 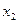 | 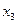 | … | 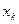 |
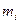 – частоты – частоты | 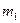 | 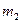 | 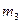 | … |  |
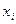 –ход эксперимента –ход эксперимента | 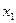 | 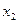 | 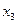 | … | 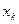 |
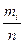 – относительные частоты – относительные частоты | 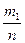 | 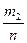 | 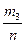 | … | 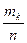 |
Если изучается непрерывная случайная величина, то группировка заключается в разбиении интервала наблюдаемых значений случайной величины на 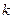 частичных интервалов равной длины
частичных интервалов равной длины 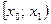 ,
, 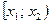 ,
, 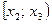 , …,
, …, 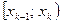 и подсчете частоты
и подсчете частоты 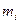 или относительной частоты
или относительной частоты 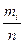 попадания наблюдаемых значений в частичные интервалы. Количество интервалов, как правило, рассчитывается по формуле:
попадания наблюдаемых значений в частичные интервалы. Количество интервалов, как правило, рассчитывается по формуле:
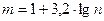 . (25.1)
. (25.1)
Длина частичного интервала вычисляется по формуле: 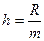 , (25.2)
, (25.2)
где 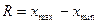 – размах вариации.
– размах вариации.
В результате составляется интервальный статистический ряд следующего вида 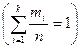 :
:
Интервалы наблюдаемых значений СВ 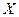 | 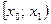 | 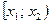 | … | 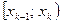 |
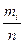 – относительные частоты – относительные частоты | 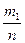 | 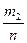 | … | 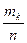 |
Определение 25.1. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
 2014-02-02
2014-02-02 1408
1408
