Общий вид степенного уравнения регрессии:
 .
.
Логарифмирование данного уравнения приводит его к линейному виду:

Оценки параметров a и b уравнения могут быть найдены МНК. Система нормальных уравнений имеет вид:
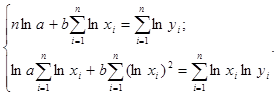
Параметр b определяется из системы, а параметр a – потенцированием выражения lna.
Показателем тесноты нелинейной корреляции является индекс корреляции, вычисляемый по формуле:
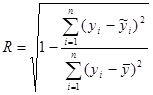 ,
,
где 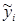 - индивидуальные значения у по уравнению связи.
- индивидуальные значения у по уравнению связи.
Индекс корреляции находится в границах: 0 < R < 1 и чемближе к единице, тем теснее связь рассматриваемых признаков, более надежно найденное уравнение регрессии.
Индекс детерминации R2 используется для проверки статистической значимости в целом уравнения нелинейной регрессии по 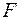 -критерию Фишера:
-критерию Фишера:
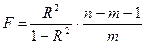 ,
,
где 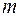 – число параметров при переменных х;
– число параметров при переменных х; 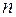 – число наблюдений.
– число наблюдений.
Если 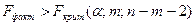 , то гипотеза Н0 о статистической не значимости уравнения регрессии отклоняется.
, то гипотеза Н0 о статистической не значимости уравнения регрессии отклоняется.
Для степенной функции  , гиперболы
, гиперболы 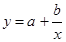 , экспоненты
, экспоненты 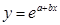 формула
формула 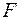 -критерия имеет вид:
-критерия имеет вид:
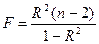 .
.
Для параболы второй степени 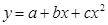 :
:
 .
.
 2014-02-02
2014-02-02 1057
1057







