Индекс детерминации

Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, R ² имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R ² для нелинейных связей называют индексом детерминации.

Оценка статистической значимости индекса корреляции проводится так же, как и оценка значимости коэффициента корреляции.

Индекс детерминации R ² используется для проверки статистической значимости в целом уравнении нелинейной регрессии по F -критерию Фишера.

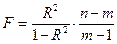
где n – число наблюдений; m – число параметров уравнения регрессии.

Величина m-1 характеризует число степеней свободы для факторной суммы квадратов, а (n – m) – число степеней свободы для остаточной суммы квадратов.

Расчет F -критерия можно вести и в таблице дисперсионного анализа результатов регрессии, как

Индекс детерминации R ² можно сравнивать с коэффициентом детерминации r ² для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации r ² меньше индекса детерминации Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если величина (R ² – r ²) не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия между R ² и r ², вычисленных по одним и тем же исходным данным, через критерий Стьюдента:

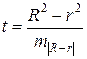
где m _{! R – r !} – ошибка разности определяемая по формуле

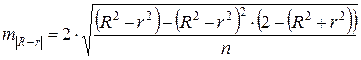
Если t _факт > t _табл, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически если величина t < 2, то различия между R и r несущественны, и, следовательно, возможно применение линейной регрессии, даже если есть предположения о некоторой нелинейности рассматриваемых соотношений признаков фактора и результата.