2014-02-02
1151
1. Строим матрицу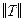 
, состоящую из всех пар номеров (i, j), для которых р (i, j) ¹ 0 (т.е. в автомате есть переход из а i в а j или наоборот) и i < j. Для каждой пары в матрице 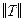указываем ее вес р (i, j), совпадающий с весом ребра соединяющего а i и а j.
| i | j | p(i,j) | ||
| T | = | |||
2. Упорядочим строки матрицы 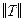, для чего построим матрицу 
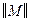следующим образом. В первую строку матрицы 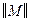поместим пару (a,b) с наибольшим весом р (a,b). В нашем случае (a,b) = (2,3), р (2,3) = 3. Из всех пар, имеющих общий компонент с парой (a,b) выбирается пара (g,d) с наибольшим весом и заносится во вторую строку матрицы 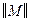. Ясно, что { a,b }×{ g,d }¹0. Затем из всех пар, имеющих общий компонент хотя бы с одной из внесенных уже в матрицу 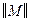пар выбирается пара с наибольшим весом и заносится в матрицу 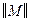и т.д.. В случае равенства весов пар вычисляются суммы весов компонентов пар (весом р (a) компонента a называется число появлений a в матрице 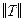) и в матрицу 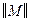заносится пара с наибольшей суммой весов. В рассматриваемом автомате на второе место вслед за парой (2,3) претендуют пары: (1,2) с р (1,2) = 2; (3,4) с р (3,4) = 2, (3,5) с р (3,5) = 2.
Для определения того, какая пара займет второе место в матрице 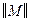находим веса компонентов пар:
р (1) = 3 р (2) = 3 р (1) + р (2) = 6
р (3) = 4 р (4) = 2 р (3) + р (4) = 6
р (3) = 4 р (5) = 2 р (3) + р (5) = 6
В данном случае для всех пар совпадают и их веса и веса их компонентов. Поэтому на второе место матрицы 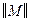может быть поставлена любая из пар (1,2), (3,4), (3,5). Но тогда на 3-м и 4-м будут остальные две. Выполнив упорядочивание всех пар, получим матрицу 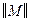в виде:
| i | j | p(i,j) | ||
| M | = | |||
3. Определяем разрядность кода для кодирования состояний автомата (количество элементов памяти – триггеров). Всего состояний M=5. Тогда
R = ]log2M[ = ]log25[ =3.
Закодируем состояния из первой строки матрицы следующим образом: K 2 = K (а 2) = 000; K 3 = K (а 3) = 001.
Для удобства кодирования будем иллюстрировать этот процесс картой Карно:
 |
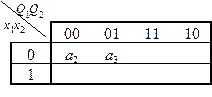4. Вычеркнем из матрицы 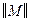первую строку, соответствующую закодированным состояниям а 2 и а 3. Получим матрицу .
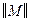| i | j | p(i,j) | ||
| M’ | = | |||
5. В силу упорядочивания п.2 в первой строке закодирован ровно один элемент. Выберем из первой строки незакодированный элемент и обозначим его g. (В нашем случае g = 1).
6. Строим матрицу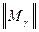 
, выбрав из 
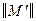строчки, содержащие g.
| i | j | p(i,j) | ||||
| M g | = | M’ | = | |||
Пусть Bg = { g 1,..., gF } – множество элементов из матрицы 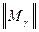, которые уже закодированы. Их коды Кg 1,..., KgF соответственно. В нашем случае:
Bg = B 3 = {2,3} K 2 = 000 K 3 = 001.
7. Для каждого Kgf (f =1,..., F) найдем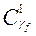 
– множество кодов, соседних с 
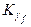и еще не занятых для кодирования состояний автомата. (Для соседних кодов кодовое расстояние d=1).
K 2 = 000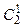 
= {100, 010}
K 3 = 001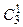 
= {011, 101}.
Построим множество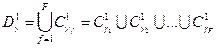 
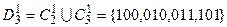
Если оказывается, что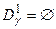 
, то строим новое множество 
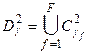, где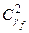 
– множество кодов, у которых кодовое расстояние до кода 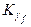равно 2 и т.д..
8. Для каждого кода из множества Dg находим кодовое расстояние до кода .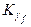
K 2 = 000 K 3 = 001
d (100, 000) = 1 d (100, 001) = 2
d (010, 000) = 1 d (010, 001) = 2
d (011, 000) = 2 d (011, 001) = 1
d (101, 000) = 2 d (100, 001) = 1
9. Находим значение функции w для каждого кода из множества Dg.
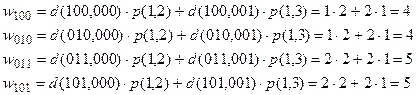
10. Из множества Dg выбираем код Kg, у которого получилось минимальное значение w в п.9. Выбираем код для состояния a 1 К 1 =100.
 |
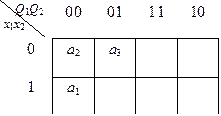11. Из матрицы 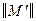вычеркиваем строки, в которых оба элемента уже закодированы, в результате чего получим новую матрицу 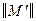. Если в новой матрице 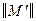не осталось ни одной строки, то кодирование закончено. В противном случае возвращаемся к п.5. В нашем случае имеем:
| i | j | p(i,j) | ||
| M’ | = | |||
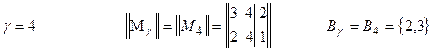
К 2 = 000 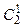= {010}
K 3 = 001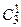 
= {011, 101}
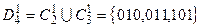
K 2 = 000 K 3 = 001
d (010, 000) = 1 d (010, 001) = 2
d (011, 000) = 2 d (011, 001) = 1
d (101, 000) = 2 d (101, 001) = 1
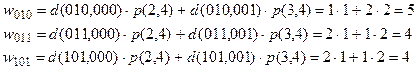
Выбираем К 4 = 101.
 |
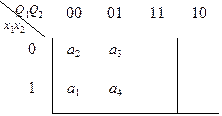К 1 = 100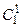 
= {110}
K 2 = 000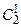 
= {010}
К 3 = 001 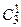= {011}
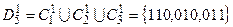
К 1 = 100 K 2 = 000 K 3 = 001
d (110, 100) = 1 d (110, 000) = 2 d (110, 001) = 3
d (010, 100) = 2 d (010, 000) = 1 d (010, 001) = 2
d (011, 100) = 3 d (011, 000) = 2 d (011, 001) = 1
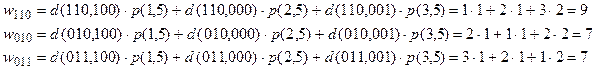
Выбираем К 5 = 011.
 |
Т.к. все состояния автомата закодированы, то работа алгоритма заканчивается. Общее количество переключений триггеров:
Минимально возможное количество переключений (если бы состояния были закодированы соседним кодированием)
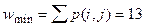
Коэффициент эффективности кодирования:
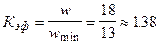
Рассмотренный алгоритм кодирования является машино-ориентированным, существуют программы, реализующие этот алгоритм.
Необходимо отметить в заключении, что использование алгоритма кодирования обеспечивает наиболее простую с точки зрения реализации схему, но при этом возможны гонки. Для радикального устранения последних используют аппаратные методы – триггеры с двойной памятью: триггеры, управляемые фронтом и т.д..
