Кабели
Значения 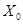 кабелей обычно находят по заводским данным, приводимым в справочной литературе.
кабелей обычно находят по заводским данным, приводимым в справочной литературе.
Для кабелей в зависимости от пути тока нулевой последовательности (только по оболочке или по оболочке и в земле) сопротивление нулевой последовательности ориентировочно находится в пределах 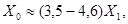
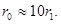
4.4. Порядок составления схем замещения отдельных последовательностей
4.4.1 Общие замечания
При использовании метода симметричных составляющих к расчету любого несимметричного режима одной из первоочередных задач является составление схем замещения в общем случае всех трех последовательностей (прямой, обратной и нулевой).
При аналитическом решении поставленной задачи по этим схемам находят результирующие сопротивления отдельных последовательностей рассматриваемой системы относительно места, где возникла несимметрия. Из схемы замещения прямой последовательности, помимо того, определяют результирующую э.д.с. относительно той же точки.
Схемы замещения отдельных последовательностей составляют в соответствии с указаниями § 2.2.4.
В частности, сопротивления и э.д.с. элементов схем замещения выражают в именованных или относительных единицах, приводя их соответственно к выбранной основной ступени напряжения или к выбранным базисным условиям.
4.4.2. Порядок сставления схем замещения
прямой и обратной последовательностей
Схема замещения прямой последовательности является обычной схемой, которую составляют для расчета любого симметричного трехфазного режима.
В зависимости от применяемого метода расчета и рассматриваемого момента времени в нее вводят генераторы и нагрузки соответствующими реактивностями и э.д.с. Все остальные элементы вводят в схему замещения неизменными сопротивлениями.
Поскольку пути циркуляции токов обратной последовательности те же, что и токов прямой последовательности, схема замещения обратной последовательности по структуре аналогична схеме прямой последовательности.
Различие между ними состоит прежде всего в том, что в схеме обратной последовательности э.д.с. всех генераторных ветвей условно приинимают равными нулю (см.§ 4.3) и кроме того, считают, что реактивности обратной последовательности электрических машин и обобщенных нагрузок постоянны и не зависят от вида и условий возникшей несимметрии, а также от рассматриваемого момента времени.
Началом схемы прямой и обратной последовательностей считают точку, в которой объединены свободные концы всех генерирующих и нагрузочных ветвей. Это точка нулевого потенциала схемы соответствующей последовательности.
Концом схемы прямой или обратной последовательностей считают точку, где возникла рассматриваемая несимметрия.
При продольной несимметрии каждая из схем имеет два конца; ими яв-
ляются две точки, между которыми расположена данная продольная несим-
метрия.
К концу или между концами схем отдельных последовательностей приложены напряжения соответствующих последовательностей, возникающие в месте несимметрии.
4.4.3.Порядок составления схемы замещения нулевой последовательности
Токи нулевой последовательности по существу являются однофазным током, разветвленным между тремя фазами (векторы токов нулевой последовательности имеют одинаковое направление во всех фазах) и воз-
вращающимся через землю и параллельные ей цепи.
В этой связи, путь циркуляции токов нулевой последовательности резко отличается от пути, по которому проходят токи прямой и обратной последовательностей.
Конфигурация схемы замещения нулевой последовательности в значительной мере определяется видом соединений обмоток трансформа-торов и автотрансформаторов.
Составление схемы замещения нулевой последовательности следует начинать от точки где возникла несимметрия, считая, что в этой точке все фазы замкнуты между собой накоротко и к ней приложено напряжение ну-
левой последовательности. В зависимости от вида несимметрии это напря-
жение прикладывается или относительно земли (поперечная несимметрия, рис.4.3, 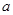 ) или последовательно в рассечку фазных проводов (продольная несимметрия, рис. 4.3,
) или последовательно в рассечку фазных проводов (продольная несимметрия, рис. 4.3,  ).
).
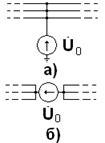 Исходя из соответствующего данной несимметрии включения напряжения нулевой поледовательности, следует выявить в пределах каждой электрически связанной цепи возможные пути протекания токов нулевой последователь-
Исходя из соответствующего данной несимметрии включения напряжения нулевой поледовательности, следует выявить в пределах каждой электрически связанной цепи возможные пути протекания токов нулевой последователь-
ности.
Следует иметь ввиду, что если напряжение нулевой после- довательности приложено относительно земли, то при от- …Рис.4.3. сутствии емкостной проводимости для циркуляции токов нулевой последовательности необходима по меньшей мере одна заземлен-
ная нейтраль в той же электрически связанной цепи, где приложено это напряжение.
При наличии нескольких заземленных нейтралей в этой цепи образуются соответственно несколько параллельных контуров для токов нулевой последовательности.
При продольной несимметрии (напряжение нулевой последовательности введено последовательно в рассечку фазных проводов) циркуляция токов нулевой последовательности возможна даже при отсутствии заземленных нейтралей, если при этом имеется замкнутый контур через обходные пути той же электрически связанной цепи (при этом в земле циркулирует наведенный ток, следуя по трассе линии).
При отсутствии таких путей протекание токов нулевой последовательно-
сти в рассматриваемых условиях возможно только в том случае, если в той же электрически связанной цепи имеются заземленные нейтрали с обеих сторон от места, где приложено напряжение нулевой последовательности.
Сопротивление, через которое заземлена нейтраль трансформатора, генератора, двигателя или нагрузки, должно быть введено в схему нулевой последовательности утроенной величиной.
Это обусловлено тем, что любую схему замещения составляют для одной фазы, а через сопротивление, включенное в нейтраль протекает сумма токов нулевой последовательности всех трех фаз.
На рис.4.4 показан пример составления схемы замещения нулевой после-
довательности для случая, когда напряжение нулевой последовательности возникает между проводами фаз и землей (поперечная несимметрия).
Обмотки трансформаторов, автотрансформатора и прочие элементы схемы рис.4.4 обозначены порядковыми номерами, которые сохранены в обозначениях элементов схемы нулевой последовательности.
Поскольку в цепи среднего напряжения автотрансформатора имеется путь для токов нулевой последовательности, автотрансформатор входит
своей полной схемой замещения. Циркуляция тока нулевой последователь-
ности в обмотке 12 трансформатора Т-2 обеспечена через заземленную ней-
траль нагрузки. Этот трансформатор предполагается трехстержневым и по-
этому учтена его реактивность намагничивания нулевой последовательно-
сти.
Для другого трансформатора и автотрансформатора указания об их кон-
струкции практически не нужны, так как они имеют обмотки, соединенные треугольником.
Если предположить, что в той же точке напряжение нулевой последова-
тельности приложено в рассечку фазных проводов, то легко убедиться в том, что в этом случае схема замещения нулевой последовательности оста-
нется прежней, но ее результирующее сопротивление будет совсем иным.

Рис.4.4.
а – расчетная схема; б – схема замещения нулевой последовательности
4.4.4. Порядок определения результирующих э.д.с. и сопротивления
Следующий этап аналитического расчета несимметричного режима заключается в определении результирующих сопротивлений схем замеще-
ния отдельных последовательностей относительно точки, где возникла не-
симметрия. Кроме этого, на этом этапе из схемы прямой последовательнос-
ти находят также результирующую э.д.с. относительно той же точки.
При этом нужно иметь в виду принципиальное различие в преобразова-
нии схем замещения при поперечной и продольной несимметриях.
Обратимся к конкретной расчетной схеме рис.4.5, 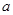 и проследим на ней за тем, в чем именно состоит это различие.
и проследим на ней за тем, в чем именно состоит это различие.
На расчетной схеме и в схемах замещения отдельных последовательнос-
тей (рис.4.5,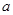 ,
, ,
,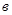 ,
,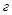 ,
, ,
, 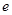 ,
,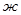 ) все элементы и сопротивления пронумерова-
) все элементы и сопротивления пронумерова-
ны.
При поперечной несимметрии в точке 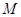 схема замещения прямой после-
схема замещения прямой после-
довательности имеет вид, представленный на рис.4.5, . Последовательно соединенные в ней сопротивления 1 и 2, а также 5 и 6 обозначены соответ-
. Последовательно соединенные в ней сопротивления 1 и 2, а также 5 и 6 обозначены соответ-
ственно номерами 8 и 9.
Для определения результирующих э.д.с. и сопротивления относительно точки 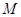 достаточно заменить ветвь 9 с
достаточно заменить ветвь 9 с 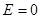 и ветвь, получаемую сложени-
и ветвь, получаемую сложени-
ем сопротивления 8 с параллельно соединеннными сопротивлениями 3 и 4 и имеющуюся э.д.с. 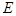 , одной эквивалентной (рис.4.5,
, одной эквивалентной (рис.4.5,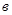 ).
).
Схема замещения обратной последовательности и ее преобразования аналогичны, за исключением того, что в ней отсутствуют э.д.с. источников.
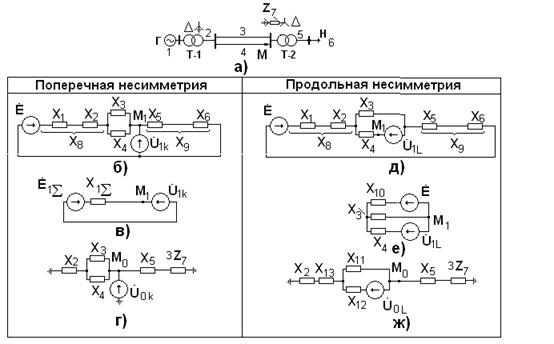
Рис.4.5.
Схему замещения нулевой последовательности (рис.4.5,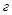 ) также легко преобразовать к результирующему сопротивлению относительно точки
) также легко преобразовать к результирующему сопротивлению относительно точки 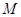 путем последовательного и параллельного сложения ветвей.
путем последовательного и параллельного сложения ветвей.
Пусть теперь в точке 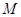 возникла продольная несимметрия.
возникла продольная несимметрия.
В этом случае напряжение прямой последовательности в точке 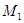 должно быть введено в рассечку цепи сопротивления 4 (рис.4.5,
должно быть введено в рассечку цепи сопротивления 4 (рис.4.5,  ).
).
Для определения результирующих э.д.с. и сопротивления схемы относи-
тельно точки 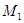 в данном случае необходимо вначале сложить последова-
в данном случае необходимо вначале сложить последова-
тельно сопротивления 8 и 9. Затем образовавшуюся ветвь 10 с э.д.с. 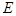 и ветвь 3 (рис.4.5,
и ветвь 3 (рис.4.5, 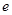 ) следует заменить эквивалентной, что дает искомую результирующую э.д.с. относительно точки
) следует заменить эквивалентной, что дает искомую результирующую э.д.с. относительно точки 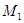 , а для нахождения результи-
, а для нахождения результи-
рующего сопротивления относительно той же точки достаточно к сопротив-
лению полученной эквивалентной ветви прибавить сопротивление 4.
Схема замещения обратной последовательности аналогична схеме рис.4.5, ; в ней лишь отсутствует э.д.с. источника. Ее результирующее сопротивление относительно точки
; в ней лишь отсутствует э.д.с. источника. Ее результирующее сопротивление относительно точки  находится также как и схемы замещения прямой последовательности.
находится также как и схемы замещения прямой последовательности.
В схему замещения нулевой последовательности (рис.4.5, 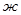 ) двухцепная линия введена своей трехлучевой схемой замещения с сопротивлениями 11, 12 и 13 (см. Приложение П-8 [4]) c тем, чтобы учесть взаимоиндукцию между цепями, находящимися теперь в различных условиях.
) двухцепная линия введена своей трехлучевой схемой замещения с сопротивлениями 11, 12 и 13 (см. Приложение П-8 [4]) c тем, чтобы учесть взаимоиндукцию между цепями, находящимися теперь в различных условиях.
Для определения результирующего сопротивления схемы относительно точки 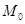 нужно сопротивление 11 сложить параллельно с суммой сопротивлений 2, 13, 5 и 7 (сопротивление 7 входит утроенной величиной) и затем прибавить сопротивление 12.
нужно сопротивление 11 сложить параллельно с суммой сопротивлений 2, 13, 5 и 7 (сопротивление 7 входит утроенной величиной) и затем прибавить сопротивление 12.
4.5. Учет влияния трансформации на распределение токов и напряжений
Фазные токи и напряжения при несимметричных режимах проще всего находить путем суммирования их симметричных составляющих.
Поскольку рассматриваемые трехфазные схемы предполагаются выполненными симметрично, то распределение токов и напряжений каждой последовательности находят в схеме замещения одноименной последовательности, руководствуясь правилами и законами распределения токов и напряжений в линейных электрических цепях[1].
При определении фазных величин за трансформаторами нужно иметь в виду, что векторы токов и напряжений при переходе через трансформатор изменяются не только по величине, но и по фазе в зависимости от вида соединения его обмоток.
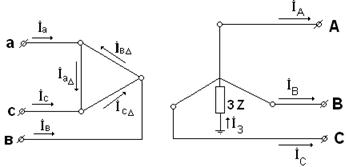
Обратимся к рис.4.6, где приведена принципиальная схема траносформатора с соединением обмоток звезда с заземленной нейтралью/треугольник.
 |
Если число витков фазных обмоток соответственно равны
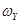 и
и 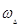 , то линейный коэффициент трансформации будет
, то линейный коэффициент трансформации будет 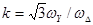 .
. Рис.4.6.
При заданных фазных токах 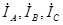 звезды и в соответствии с принятыми на рис. 4.6 положительными направлениями для токов в линейных проводах за треугольником имеем:
звезды и в соответствии с принятыми на рис. 4.6 положительными направлениями для токов в линейных проводах за треугольником имеем:
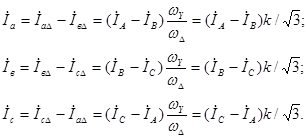 (4.13)
(4.13)
Эту запись можно видоизменить, выразив токи через их симметричные составляющие.
Так, например для тока 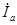 получим
получим
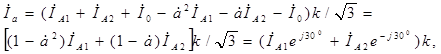 (4.14)
(4.14)
откуда, в частности, видно, что линейные токи на стороне обмотки трансформатора, соединенной в треугольник, не содержат составляющих нулевой последовательсти.
Аналогично могут быть найдены напряжения на стороне обмотки трансформатора, соединенной в треугольник.
Если 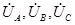 - фазные напряжения со стороны звезды, включающие в себя и падения напряжения в самом трансформаторе, то искомые фазные напряжения со стороны треугольника будут:
- фазные напряжения со стороны звезды, включающие в себя и падения напряжения в самом трансформаторе, то искомые фазные напряжения со стороны треугольника будут:
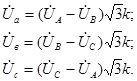 (4.15)
(4.15)
При выражении напряжений через симметричные составляющие, напрмер, для напряжения 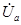 , будем иметь:
, будем иметь:

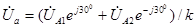 . (4.16)
. (4.16)
Структура выражений (4.14) и (4.16) показывает, что при переходе со стороны звезды на сторону треугольника трансформатора, обмотки которого соединены по группе 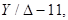 векторы прямой последовательности повертываются на
векторы прямой последовательности повертываются на 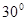 в направлении вращения векторов (против направления движения стрелки часов), а векторы обратной последовательности – на
в направлении вращения векторов (против направления движения стрелки часов), а векторы обратной последовательности – на 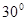
в противоположном направлении (рис.4.7-4.8).
При переходе через трансформатор в обратном направлении угловые смещения симметричных составляющих меняют свой знак на противоположный.

Рис.4.7. Рис.4.8.
4.6. Анализ отдельных видов несимметричных коротких замыканий
4.6.1. Двухфазное короткое замыкание
Для наглядности и удобства рассуждений короткие замыкания будут рассматриваться на отпайках, отходящих от фазных проводов, причем сопротивления проводов отпаек принимаются равными нулю (рис.4.9).
При двухфазном к.з. токи нулевой последовательности отсутствуют и поэтому для его анализа достаточно иметь только две схемы замещения: прямой и обратной последовательностей.
Предположим, что эти схемы замещения уже составлены, приведены к простейшему виду и известны их результирующие 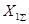 и
и 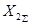 , а также
, а также 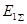 .
.
 |
Для дальнейших рассуждений воспользуемся схемой рис. 4.10.
Рис.4.9. Рис.4.10.
Уравнения (4.8)-(4.9) дают лишь две связи между четырьмя неизвестными, поэтому для их решения нужны еще два уравнения, которые получают из граничных условий для двухфазного к.з.:
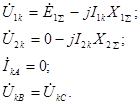 (4.17)
(4.17)
Система уравнений составлена для фазы 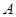 , но она имеет силу для любой другой фазы.
, но она имеет силу для любой другой фазы.
При записи граничных условий для всех видов несимметрии принимают, что фаза 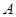 находится в условиях отличных от условий для двух других фаз, то есть она является, как говорят, особой фазой.
находится в условиях отличных от условий для двух других фаз, то есть она является, как говорят, особой фазой.
За положительное направление фазных токов и их симметричных составляющих принимают направление к месту короткого замыкания.
В дальнейшем условимся при записи симметричных составляющих фазы 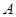 не указывать индекс фазы.
не указывать индекс фазы.
Согласно системе уравнений (4.2) 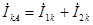 , но из (4.17)
, но из (4.17)  ,
,
следовательно, 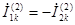 . (4.18)
. (4.18)
Согласно (4.3)-(4.5)
 (4.19)
(4.19)
Используя (4.17)-(4.19), можно записать:
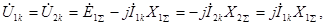
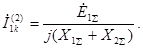 (4.20)
(4.20)
Согласно (4.2) токи в фазах будут:
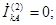
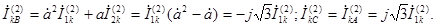 (4.21)
(4.21)
Симметричные составляющие напряжения для фазы 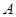 при двухфазном к.з. определим согласно формул (4.17)-(4.19):
при двухфазном к.з. определим согласно формул (4.17)-(4.19):
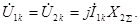
Тогда в соответствии с (4.2) напряжения фаз будут:
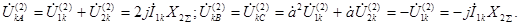 (4.22)
(4.22)
Заметим, что напряжение неповрежденной фазы в два раза больше по модулю напряжения поврежденных фаз и противоположно по знаку.
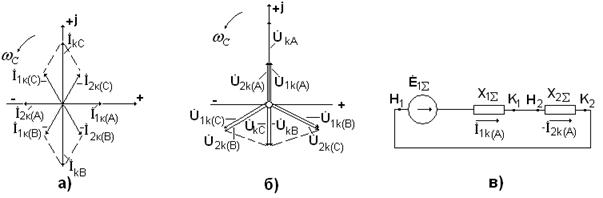
На рис. 4.11 представлены векторные диаграммы токов, напряжений и комплексная схема замещения при двухфазном к.з. в точке К.
Рис.4.11.
а – векторная диаграмма токов;
б – векторная диаграмма напряжений;
в – комплексная cхема замещения
Комплексная схема замещения предназначена для расчетов несиметричных режимов на расчетных столах переменного и постоянного тока.
Конфигурация комплексной схемы замещения определяется по выражению для тока прямой последовательности для рассматриваемого вида несимметрии.
Условные обозначения на комплексной схеме замещения: 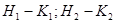 и т.д. служат для фиксации начала (
и т.д. служат для фиксации начала (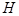 ) и конца набранной на расчетном столе схемы замещения соответствующей последовательности.
) и конца набранной на расчетном столе схемы замещения соответствующей последовательности.
По измерениям, проводимым на комлексной схеме замещения, набранной на расчетном столе постоянного тока, можно определить модули токов и напряжений всех последовательностей для фазы 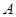 .
.
Зная из анализа каждого вида несимметрии положение векторов токов и напряжений всех последовательностей для фазы 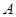 на соответствующих векторных диаграммах, далее строят системы векторов симметричных составляющих токов и напряжений для всех фаз и получают по ним искомые векторы полных фазных величин.
на соответствующих векторных диаграммах, далее строят системы векторов симметричных составляющих токов и напряжений для всех фаз и получают по ним искомые векторы полных фазных величин.
Так, для рассматриваемого вида несимметричного к.з. достаточно применить в комлексной схеме замещения только два измерительных прибора: амперметр, включаемый в разрыв последовательной цепи и вольтметр, подключаемый к точкам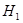 и
и 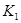 .
.
При этом, первый прибор покажет значение модуля тока прямой последовательности фазы 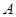 , второй – модуля напряжения прямой последовательности фазы
, второй – модуля напряжения прямой последовательности фазы 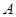 .
.
Таким образом, ценность применения комплексных схем замещения состоит в простоте определения искомых фазных величин в любой точке длясети любой сложности, схемы замещения соответствующих последовательностей которой набраны и соединены между собой соответствующим образом на расчетном столе.
4.6.2. Однофазное короткое замыкание на землю
Для этого вида к.з. (см. рис.4.12) нужно иметь три схемы замещения –
прямой обратной и нулевой последовательностей.
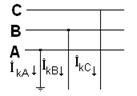 Будем по прежнему считать, что эти схемы замещения приведены к простейшему виду и нам известны
Будем по прежнему считать, что эти схемы замещения приведены к простейшему виду и нам известны 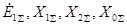 .
.
Для этого случая к.з. с учетом граничных условий можно записать следующие уравнения
Рис.4.12.
 |
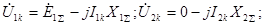
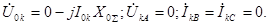 (4.23) Согласно (4.3)-(4.5) и (4.23) имеем:
(4.23) Согласно (4.3)-(4.5) и (4.23) имеем: 
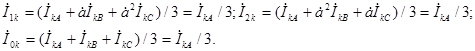
Следовательно, 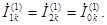 (4.24)
(4.24)
Согласно (4.2) и (4.23) имеем: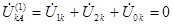 , а используя (4.24), получим:
, а используя (4.24), получим: 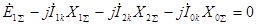 .
.
Таким образом, 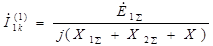 . (4.25)
. (4.25)
Токи в фазах согласно (4.23)-(4.24) будут:
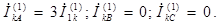 (4.26)
(4.26)
Ток в земле будет равен:
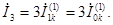 (4.27)
(4.27)
Напряжения фаз
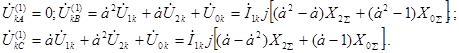 (4.28)
(4.28)
На рис. 4.13 представлены векторные диаграммы токов, напряжений и комплексная схема замещения при однофазном коротком замыкании на землю в точке 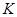 .
.
Векторная диаграмма токов строится на основании формулы (4.24), а напряжений – исходя из того, что 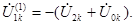

Угол 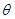 между векторами
между векторами  и
и 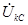 изменяется от 60 до
изменяется от 60 до 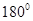 .
.
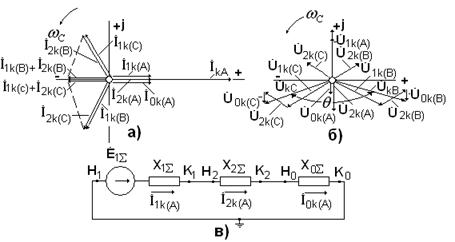 |
Рис.4.13.
а - векторная диаграмма токов;
б – векторная диаграмма напряжений;
в – комплексная схема замещения
4.6.3. Двухфазное короткое замыкание на землю
Для этого вида к.з. (см. рис.4.14) нужно иметь три схемы замещения – прямой обратной и нулевой последовательностей.
Будем по прежнему считать, что эти схемы замещения приведены к простейшему виду и нам известны 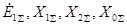 .
.
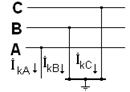 Для этого вида к.з. уравнения связи с учетом граничных условий запишутся в следующем виде:
Для этого вида к.з. уравнения связи с учетом граничных условий запишутся в следующем виде: 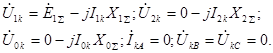 (4.29) Согласно (4.3)-(4.5) и (4.29) имеем:
(4.29) Согласно (4.3)-(4.5) и (4.29) имеем:
Рис.4.14.  . (4.30)
. (4.30)
Из (4.29) следует, что:
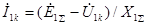 ;
; 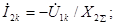
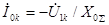 .
.
Так как 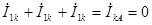 ,
,
то 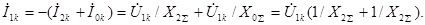
Подставляя выражение для  из последнего выражения в (4.29), получим
из последнего выражения в (4.29), получим 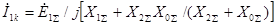 ;
; 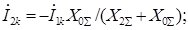

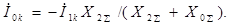 (4.31)
(4.31)
Токи в фазах при двухфазном к.з.на землю будут:
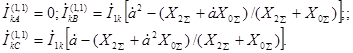 . (4.32)
. (4.32)
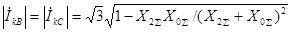 . (4.33)
. (4.33)
Ток в земле при двухфазном к.з. на землю
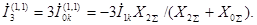 (4.34)
(4.34)
Напряжения фаз
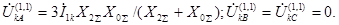 (4.35)
(4.35)
 |
На рис. 4.15 представлены векторные диаграммы токов, напряжений и комплексная схема замещения при двухфазном коротком замыкании на землю в точке К.
Рис.4.15.
а – векторная диаграмма токов;
б – векторнафя диаграмма напряжений;
в – комплексная схема замещения
4.7. Обобщение результатов
анализа отдельных видов несимметричных коротких замыканий
Если рассмотреть формулы (4.20), (4.25) и (4.32), приняв во внимание только модуль значения составляющей тока прямой последовательности, то можно видеть:
 (4.36)
(4.36)
Как следует из (4.36), для каждого из значений тока прямой последова-
тельности структурно можно записать выражение:
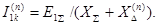 (4.37)
(4.37)
Выражение (4.37) позволило Н.Н.Щедрину сделать обобщение [5]:
“ Ток прямой последовательности при любом несимметричном к.з. может быть определен как ток трехфазного к.з. в точке, удаленной от действи-
тельной точки к.з. на дополнительную реактивность 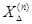 , которая не за-
, которая не за-
висит от параметров схемы прямой последовательности и для каждого вида к.з. в рассматриваемой точке остается неизменной для всего процес-
са к.з.”
Из формул (4.21), (4.26) и (4.2) модули значений токов в поврежденных фазах будут равны:
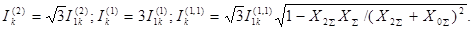 (4.38)
(4.38)
Из (4.38) следует, что структурно общей формулой для токов в повреж-
денных фазах при любом виде к.з. может служить выражение:
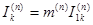 . (4.39)
. (4.39)
Исходя из выражений (4.37) и (4.39) для определения токов в поврежденных фазах при различных видах к.з., нужно использовать данные, приведенные в табл.4.3.
Таблица 4.3
Значения дополнительной реактивности 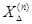 и множителя
и множителя 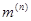
| Вид короткого замыкания | 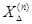 | 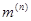 |
| Трехфазное | ||
| Двухфазное | 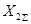 | 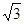 |
| Однофазное на землю |  | |
| Двухфазное на землю | 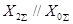 | 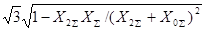 |
Как следует из (4.37)-(4.38), для вычисления несимметричных токов к.з. можно использовать все приемы, применяемые при расчете тока трехфазно-
го к.з.
Например, при расчете несимметричного к.з. по расчетным кривым при-
меняют те же расчетные кривые, по которым рассчитывают ток трехфазно-
го к.з.
При этом расчетная реактивность 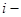 той независимой генерирующей ветви источника при использовании расчетных кривых для определения тока несимметричного к.з. рассчитывается по формуле:
той независимой генерирующей ветви источника при использовании расчетных кривых для определения тока несимметричного к.з. рассчитывается по формуле:
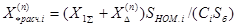 . (4.40)
. (4.40)
Следует иметь в виду, что при использовании приемов расчета тока трехфазного к.з. для расчета тока несимметричного к.з. вида 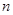 определяется только ток прямой последовательности
определяется только ток прямой последовательности 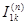 .
.
Так, например, по расчетным кривым находится только ток прямой последовательности 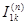 .Чтобы найти токи в поврежденных фазах при несимметричном к.з. вида
.Чтобы найти токи в поврежденных фазах при несимметричном к.з. вида 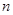 , нужно найденный по расчетным кривым ток прямой последовательности
, нужно найденный по расчетным кривым ток прямой последовательности 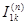 умножить на множитель
умножить на множитель 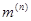 .
.
4.8. Учет переходного сопротивления в месте замыкания
Известно, что электрическую дугу на открытом воздухе в первом приближении можно характеризовать активным сопротивлением  .
.
Рассмотрим пути учета сопротивления дуги при различных видах несимметричных к.з.
Пусть замыкание между фазами  и
и  произошло через сопротивление дуги
произошло через сопротивление дуги 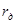 .
.
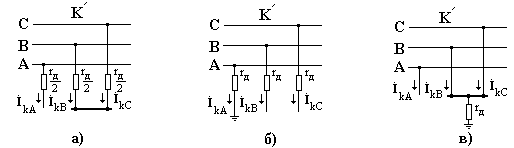 |
Его можно представить как глухое двухфазное к.з. на ответвлении, фазы которого имеют одинаковые сопротивления
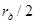 (рис.4.16,
(рис.4.16,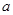 ).
). Рис.4.16.
Таким приемом несимметричный участок трехфазной цепи приведен к симметричному (хотя в фазе 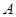 , на самом деле, отсутствует
, на самом деле, отсутствует 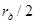 ).
).
Введение сопротивления 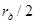 в фазу
в фазу 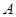 , очевидно, не меняет условий рассматриваемого вида замыкания, поскольку на данном участке ток в этой фазе отсутствует.
, очевидно, не меняет условий рассматриваемого вида замыкания, поскольку на данном участке ток в этой фазе отсутствует.
Считая, как и ранее, остальную часть схемы чисто индуктивной, по аналогии с (4.20) для тока прямой последовательности в месте замыкания можно записать:
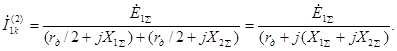 (4.41)
(4.41)
Для напряжения прямой последовательности за сопротивлением дуги 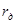
(точка 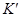 ) имеем:
) имеем:
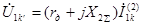 .
.  (4.42)
(4.42)
для напряжения обратной последовательности в точке 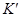 справедливо выражение
справедливо выражение 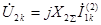 . (4.43)
. (4.43)
 2014-02-02
2014-02-02 3343
3343
