Хроматическое число

Раскраски

Гипотезу четырех красок можно с полным основанием назвать еще «болезнью четырех красок», так как она во многом похожа на заболевание. Она в высшей степени заразна. Иногда она протекает сравнительно легко, но в некоторых случаях, приобретает затяжной или даже угрожающий характер. Никаких прививок против нее не существует; правда, люди с достаточно здоровым организмом после короткой вспышки приобретают пожизненный иммунитет. Этой болезнью человек может болеть несколько раз, и она подчас сопровождается острой болью, но ни одного летального исхода зарегистрировано не было. Известен, по крайней мере один случай передачи болезни от отца к сыну, так что, может быть, она наследственна.

Тем не менее, именно попытки обосновать эту гипотезу стимулировали получение ряда результатов по раскраске графов, которые в свою очередь привели к исследованиям некоторых других разделов теории графов.

В этой главе после определения раскраски графа и его хроматического числа излагается доказательство теоремы о пяти красках, а затем обсуждается гипотеза четырех красок. Далее вводятся однозначно раскрашиваемые графы, т. е. графы, которые можно раскрасить единственным образом, а также критические графы (минимальные относительно раскраски). Исследуется тесная взаимосвязь между гомоморфизмами и раскрасками. Глава завершается описанием свойств хроматического многочлена.

Раскраской графа называется такое приписывание цветов его вершинам, что никакие две смежные вершины не получают одинакового цвета. Множество всех вершин одного цвета является независимым и называется одноцветным классом. В n-раскраске графа G используется n цветов, таким образом, эта раскраска разбивает V на n одноцветных классов. Хроматическое число хr (G) графа G определяется как наименьшее n, для которого граф G имеет n-раскраску. Граф G называется n-раскрашиваемым, если хr(G)<n, и n-хроматическим, если xr(G)=n

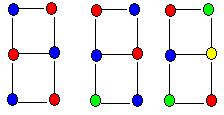
Поскольку граф G, очевидно, имеет n-раскраску и хr(G)-раскраску, он должен иметь также n-раскраску для любого п, удовлетворяющего неравенствам хr(G)<n<p. Граф на рисунке является 2-хроматическим. На этом же рисунке приведены n-раскраски для п=2, 3, 4;

Легко найти хроматические числа некоторых известных графов:

xr(КР)=Р, хr(Кр-х)=р-1, хr(!Кр) = 1, хr(Кm,n)=2, хr(С2n)=2, xr(C2n+i)=3 и хr(Т)=2 для любого нетривиального дерева Т.

Очевидно, что граф является 1-хроматическим тогда и только тогда, когда он вполне несвязен. Описание двуцветных (2-раскрашиваемых) графов дано Кёнигом и отражено в теореме

Теорема. Граф двуцветен тогда и только тогда, когда он не содержит нечетных простых циклов.

Похоже, что проблема характеризации n-цветных графов для n> 3 все еще не решена, поскольку такой критерий даже дляn=3 помог бы решить гипотезу четырех красок. Не найдены также эффективные методы определения хроматического числа произвольного графа. Однако известно несколько оценок для xr(G), в которых используются различные другие инварианты. Одна очевидная нижняя оценка — это число вершин в полном наибольшем подграфе графа G. Мы рассмотрим сейчас верхние оценки; первая такая оценка была получена Секерешем и Вилфом

Теорема. Для любого графа G хr(С)<1+mахd(С'),где максимум берется по всем порожденным подграфам G' графа G.

С ледстви е (а). Для любого графа G хроматическое число не больше чем на 1 превышает максимальную степень:

xr < 1 + D

Брукс показал, однако, что часто эту оценку можно улучшить.

Теорема. ЕслиD(G)=n, то граф G всегда n-раскрашиваем, за исключением следующих двух случаев:

1) n=2 и G имеет компоненту, являющуюся нечетным циклом',

2) n> 2 и Кn+1— компонента графа G.

Теорема. Для любого графа G p/b₀<xr<p-b₀ + 1

Исследуя приведенные выше рассуждения, легко проникнуться верой в то, что все графы с большим хроматическим числом имеют большие клики и, следовательно, содержат треугольники. И вот Дирак поставил вопрос, существует ли граф без треугольников, но с произвольно большим хроматическим числом. Положительно на этот вопрос ответили независимо друг от друга Бланш Декарт, Зыков и Мыцельский. Затем их результат обобщили Дж. и Л. Келли, доказав, что для любого п> 2 существует n-хроматический граф, обхват которого превосходит 5. Они предположили, что справедливо следующее утверждение, которое первым доказал Эрдёш, используя вероятностные соображения. Позже Ловац дал конструктивное доказательство этой теоремы.

Теорема. Для любых двух положительных целых чисел t и n существует n-хроматический граф, обхват которого превосходит t.