Вторичные параметры линий

Волновое сопротивление 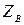определяется через первичные параметры по следующей формуле:

.

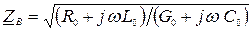Если сопротивление нагрузки 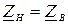, то это означает, что линия нагружена согласованно. Волновое сопротивление является характеристическим, если линия рассматривается как четырехполюсник.

Существуют также приближенные формулы для расчета волнового сопротивления. Например, в области тональных частот (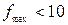кГц) будут справедливы неравенства и 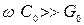, тогда

.

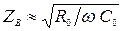В области высоких частот, где 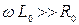и 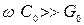, получим формулу для расчета волнового сопротивления:

.

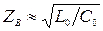Коэффициент распространения – это характеристическая постоянная передачи линии единичной длины. Характеристическая постоянная передачи является комплексным числом и в данном случае представляется как

,

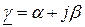где 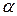– коэффициент затухания (ослабления), 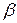– коэффициент фазы, или волновое число. В диапазоне тональных частот (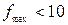кГц), где и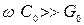

.

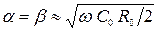В системах радио- и многоканальной связи линии используются в диапазоне частот, в котором 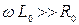и 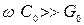. Приближенные формулы для этого случая имеют следующий вид:

;

.

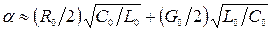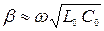Данные приближенные формулы используются при расчете вторичных параметров магистральных линий связи (коаксиальных и симметричных кабельных) и фидеров в их рабочей полосе частот. В области высоких частот где 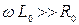и 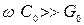, приемлемые для практики результаты расчетов получаются, если положить и 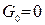. Такие линии называются линиями без потерь. В этом случае 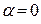, а 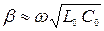. При подстановке первичных параметров в системе единиц СИ 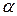получается в неперах на метр (Нп/м), а 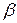– в радианах на метр (рад/м). Для того чтобы получить 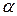в децибелах на метр (дБ/м), необходимо найденные по формулам значения 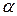умножить на 8,69.

Зная волновое сопротивление и коэффициент распространения, можно найти напряжения и ток в любом сечении линии, т. е. эти величины полностью характеризуют линию и называются вторичными параметрами.