Лекция 33.
Одним из способов повышения качества передачи сообщений по дискретным каналам с помехами является применение корректирующих кодов, позволяющих обнаруживать и исправлять ошибки, возникающие в канале. Сколько же ошибок может обнаружить и исправить код? Согласно теореме Шеннона при скорости передачи информации R меньше пропускной способности канала С существуют коды, обеспечивающие безошибочную передачу. Однако они сложны и даже еще не найдены. Предложены и используются коды, обнаруживающие и исправляющие не все, а часть ошибок.
Общий принцип построения корректирующих кодов достаточно прост. Из общего числа 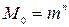 возможных кодовых комбинаций значности m и основания n используются для передачи дискретных сообщений не все, а только необходимое количество
возможных кодовых комбинаций значности m и основания n используются для передачи дискретных сообщений не все, а только необходимое количество 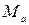 (естественно,
(естественно, 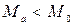 ). Используемые кодовые комбинации называются разрешенными. Остальные
). Используемые кодовые комбинации называются разрешенными. Остальные 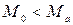 комбинаций считаются запрещенными, т. е. они не могут передаваться по каналу связи и их появление на приемном конце свидетельствует о наличии ошибок. По определению акад. А. А. Харкевича, корректирующим кодом является код, удовлетворяющий единственному условию:
комбинаций считаются запрещенными, т. е. они не могут передаваться по каналу связи и их появление на приемном конце свидетельствует о наличии ошибок. По определению акад. А. А. Харкевича, корректирующим кодом является код, удовлетворяющий единственному условию: 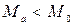 . Действительно, если имеется хотя бы одна запрещенная кодовая комбинация, то возникает принципиальная возможность обнаружения (или даже исправления) ошибок передачи.
. Действительно, если имеется хотя бы одна запрещенная кодовая комбинация, то возникает принципиальная возможность обнаружения (или даже исправления) ошибок передачи.
Таким образом, любой корректирующий код является кодом с избыточностью (имеются лишние, неиспользуемые кодовые комбинации). Для описания корректирующего кода вводятся следующие параметры:
Корректирующая способность кода определяется кратностью обнаруживаемых 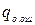 и исправляемых
и исправляемых 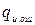 ошибок, под которыми понимают гарантированное число ошибок в кодовой комбинации, обнаруживаемых или исправляемых заданным кодом. Совершенно ясно, что чем больше кратность
ошибок, под которыми понимают гарантированное число ошибок в кодовой комбинации, обнаруживаемых или исправляемых заданным кодом. Совершенно ясно, что чем больше кратность 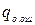 и
и 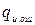 , тем совершенней является код.
, тем совершенней является код.
Расстояние Хэмминга 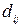 - показывает степень различия между
- показывает степень различия между 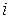 -й и
-й и 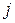 -й кодовыми комбинациями. Для любых двух двоичных кодовых комбинаций кодовое расстояние равно числу несовпадающих в них разрядов. Так, приведенные ниже комбинации (для удобства различения они написаны друг под другом)
-й кодовыми комбинациями. Для любых двух двоичных кодовых комбинаций кодовое расстояние равно числу несовпадающих в них разрядов. Так, приведенные ниже комбинации (для удобства различения они написаны друг под другом)

не совпадают в трех разрядах (помечены штрихами) и поэтому расстояние Хэмминга 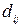 =3. Математически расстояние Хэмминга вычисляется как число единиц в сумме по модулю два этих кодовых комбинаций.
=3. Математически расстояние Хэмминга вычисляется как число единиц в сумме по модулю два этих кодовых комбинаций.
Кодовое расстояние – это минимальное расстояние Хэмминга для заданного кода. Перебрав все возможные пары разрешенных кодовых комбинаций и вычислив для них 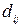 , необходимо найти среди них минимальное. Это и будет кодовое расстояние
, необходимо найти среди них минимальное. Это и будет кодовое расстояние 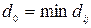 , которое полностью характеризует корректирующую способность кода.
, которое полностью характеризует корректирующую способность кода.
Вес кодовой комбинации 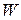 численно равен числу входящих в нее ненулевых символов.
численно равен числу входящих в нее ненулевых символов.
Относительная скорость кода 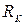 показывает относительное число разрешенных кодовых комбинаций в коде и вычисляется по формуле
показывает относительное число разрешенных кодовых комбинаций в коде и вычисляется по формуле
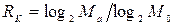
 2014-02-02
2014-02-02 3544
3544
