Процедура кодирования и декодирования для циклических кодов

Кодирующие и декодирующие устройства циклических кодов

Преобразование комбинации первичного k – разрядного кода в комбинацию циклического (n, k) – кода может быть осуществлено либо при помощи порождающего многочлена g(x), либо при помощи проверочного многочлена h(x).

а) Процедура кодирования для циклического кода по g(x).

Любой циклический (n, k) – код может быть получен в результате следующего процесса. Пусть 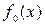- многочлен степени n -1, в качестве коэффициентов которого при степенях 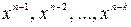выбраны информационные символы кодовой комбинации циклического (n, k) – кода, а коэффициенты при степенях х, меньших, чем n - k, равны 0. Тогда результат деления 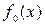на порождающий многочлен кода g(x), степень которого, как известно, равна n - k, может быть представлен в виде

,

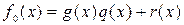где степень r(x) меньше n - k.

Образуем новый многочлен 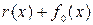, у которого коэффициенты при степенях х, меньших n - k, есть соответствующие коэффициенты r(x), а коэффициенты при остальных степенях есть соответствующие коэффициенты .

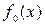Для полученного многочлена справедливо

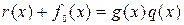
и так как его степень не превышает n -1, то по определению 2 циклического кода полученный подобным образом вектор 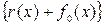принадлежит циклическому (n, k) – коду.

В векторе 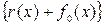коэффициентами при степенях х, равных n - k и старше, являются информационные элементы кодовой комбинации, а коэффициентами при младших степенях – проверочные (см. рис. 6.0).

Таким образом, для формирования кодовой комбинации циклического (n, k) – кода по данному способу требуется иметь устройство для умножения комбинации первичного кода, представляемой многочленом 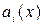степени не старшей k -1, на 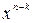, деления, полученного в результате умножения многочлена 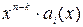степени не старшей n -1 на порождающий многочлен циклического кода g(x) степени n - k и вычисления остатка от этого деления 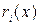степени n - k -1 и менее.

В комбинации циклического (n, k) – кода коэффициенты многочлена 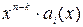(n, k) – кода являются информационными разрядами, а коэффициенты многочлена 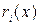- избыточными.

б) Процедура кодирования для циклического кода по h(x).

Для проверочного многочлена h(x) степени k циклического (n, k) – кода справедливо 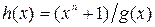или .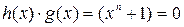

Так как по определению 2 любая кодовая комбинация кратна g(x), то для произвольной комбинации f(x) выполняется .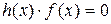

Если принять 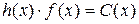, то, учитывая, что степень h(x) равна k, а степень f(x) равна n -1, для коэффициента С_с можно составить соотношение:

.

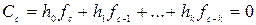Учитывая, что 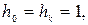находим

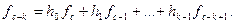
Положим с = n -1, тогда

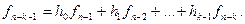
При с = n -2 имеем:

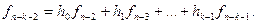
При c =k

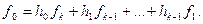
Итак, если известны коэффициенты 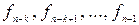, т.е. информационные элементы кодовой комбинации циклического (n, k) – кода, то при помощи систем рекуррентных соотношений, полученных выше, можно найти значение избыточных элементов 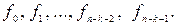Таким образом, для кодирования по проверочному многочлену необходимо иметь устройство для решения рекуррентных соотношений типа

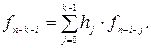
в) Процедура декодирования для циклических кодов

В основе процедуры декодирования лежит процесс выявления принадлежности принятой комбинации к множеству разрешенных кодовых комбинаций. Эта задача решается, как было показано выше, вычислением синдрома для принятой комбинации 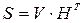. Техническая реализация этой операции может осуществляться по методике, изложенной при рассмотрении кодов Хэмминга. Однако для циклических кодов можно получить более рациональное вычисление синдрома, если использовать признак делимости каждой кодовой комбинации этих кодов на порождающий многочлен g(x). В данном случае принятая комбинация f(x) делится на порождающий многочлен g(x):

.

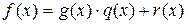Если остаток от деления r(x) =0, то считают, что комбинация f(x) и была передана.

В этом случае k коэффициентов отдаются потребителю в качестве переданного сообщения.

Если же остаток от деления 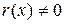, то принятая комбинация f(x) признается запрещенной и в зависимости от логики работы УЗО потребителю выдается сигнал наличия ошибки в принятой информации или организуется исправление ошибок. При исправлении по виду остатка r(x) отыскивается смежный класс, которому принадлежит принятая комбинация и определяется наиболее вероятный образец ошибки. Элементы, в которых предполагаются ошибки, инвертируются, и информационные разряды комбинации отдаются потребителям. Покажем, что остаток от деления r(x) тождественен синдрому в общепринятом определении 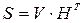. Как было показано в разделе 6.3 (пример 6.6) столбцами проверочной матрицы являются остатки от деления 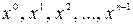на порождающий многочлен g(x).

Действительно, деление обладает свойством суперпозиции, т.е. остаток от деления некоторого многочлена f(x) степени n -1 на порождающий многочлен кода равен сумме остатков от деления степеней xⁱ с ненулевыми коэффициентами из этого многочлена (другими словами степеней xⁱ, соответствующих единицам в принятой кодовой комбинации). Произведение 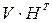сводится к суммированию столбцов матрицы Н, соответствующих единицам принятой комбинации. Учитывая, что столбцы матрицы Н – это остатки от деления xⁱ (где 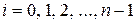), на порождающий многочлен g(x) находим, что .

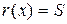Пример 6.13. Определить принадлежность комбинации 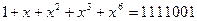циклическому (7,4) – коду с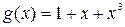

Вычисляем синдром

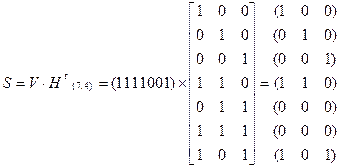
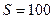1 0 0

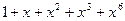Найдем остаток от деления многочлена на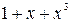

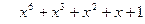
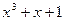
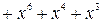
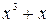
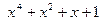
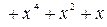
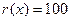
Таким образом, для вычисления синдрома 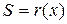необходимо иметь схему деления принятой комбинации на порождающий многочлен кода g(x).

Итак, мы установили существование двух способов вычисления синдрома для кодовых комбинаций. При этом второй способ отражает специфику представления кодовой комбинации в виде многочлена. Возможен ещё и третий способ вычисления синдрома, также вытекающий из представления кодовых комбинаций многочленами. Каждая кодовая комбинация циклического (n,k) кода кратна порождающему многочлену g(x) степени n-k. Это в свою очередь означает, что любая кодовая комбинация имеет среди своих корней n-k корней порождающего многочлена. Значит принадлежность принятой комбинации f(x) к используемому коду можно определить подстановкой вместо формальной переменной x в принятой комбинации корней порождающего многочлена g(x).

Пусть – αⁱ – корень порождающего многочлена (n,k) –кода, а f(x) – кодовая комбинация этого кода, тогда должно быть справедливо: f(x=αⁱ)=0 для всех значений i, определяющих корни g(x).

Выше отмечалось, что синдром должен определять вид ошибок, появившихся в кодовой комбинации при передаче её по каналу с помехами.

Пусть передана комбинация f(x), а принята комбинация f'(x)=f(x)+e(x), где e(x) – многочлен ошибок. Тогда f'(x=αⁱ)=f(x=αⁱ)+e(x=αⁱ)=e(x=αⁱ)=S_i

2.Если e(x) по виду совпадает с одной из кодовых комбинаций, то S_i=e(x=αⁱ)=0,

т.е. имеет место нулевой синдром, который приведёт к необнаруженной ошибке. Если же e(x) отличается от кодовой комбинации, то синдром будет ненулевым: S_i=e(x=αⁱ)≠0 и ошибка будет выявлена.

Пример 6.13. (продолжение)

Покажем, что нахождение синдрома для проверки принадлежности комбинации f(x)=1+x+x²+x³+x⁶=1111001 циклическому(7,4) – коду с g(x) = 1+x+x³ может быть осуществлено подстановкой корней многочлена g(x) вместо x в f(x).

Из приложения находим, что многочлен g(x)=1+x+x³ имеет следующие корни α¹, α²,α⁴, являющиеся элементами GF(2³). Рассмотрим результаты подстановки f(x=αⁱ), для случая i=1.

Для этого обратимся к процедуре к процедуре умножения:

(1111001)×H^T.

Обратим внимание, что матрица H^T (7,4)- кода в точности соответствует представлению элементов GF(2³) в виде ненулевых векторов в таблице задачи 6 раздела 5.8. Это не случайное совпадение. Обе эти совокупности двоичных последовательностей длины 3 получены как классы вычетов многочленов по модулю одного и того же многочлена 3-ей степени и отображают одну и ту же циклическую группу.

При этом процедура замены в проверяемом многочлене xⁱ на αⁱ и последующего суммирования результатов замены полностью эквивалентна сложению строк матрицы H^T соответствующим «1» в двоичном представлении многочлена.

Использование всех корней порождающего многочлена для формирования элементов синдрома, будут реализовано ниже в связи с понятием синдромный многочлен.

В случае исправления ошибок необходима еще и схема сопоставления синдрома образцу ошибки. В простейшем случае при исправлении однократных ошибок в основе этой схемы лежит генератор элементов поля GF(2^m).