Кері матрица. Матрица рангісі

Бізге n-ретті ерекше емес А матрица берілсін.

Анықтама. 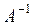матрица А матрицасының кері матрицасы деп аталады, егер 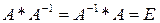(5)

теңдігі орындалса, мұндағы Е- n ретті бірлік матрица.

Теорема. (кері матрицаның бар болуы). Кез келген квадратты А матрицаның кері 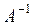матрицасы бар болуы үшін, ол матрица ерекше емес 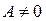матрица болуы қажетті әрі жеткілікті және ол мына төмендегі:

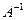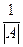
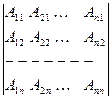= (6)

формуламен анықталады.

Мұндағы 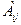берілген А матрицаның 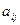элементтерінің алгебралық толықтауыштары.

Мысал. Берілген матрицаның кері матрицасын анықтаңдар

A=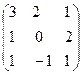

Шешуі. 1 Алдымен берілген матрицаның кері матрицасының бар болуын зерттейік. Ол үшін матрицаның анықтауышын есептейміз

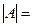
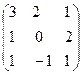=0+4-1-0-2+6=7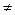0

Демек, берілген матрицаның кері матрицасы бар және оны (6) формуладан анықтаймыз.

2) Енді матрица элементтерінің алгебралық толықтауыштарын есептейік

A₁₁=(-1)¹⁺¹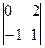=0+2=2 A₂₁=(-1)²⁺¹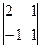=-(2+1)=-3

A₁₂=(-1)¹⁺²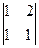=-(1-2)=1 A₂₂=(-1)²⁺²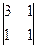=3-1=2

A₁₃=(-1)¹⁺³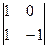=-1-0=-1 A₂₃=(-1)²⁺³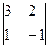=-(-3-2)=5

A₃₁=(-1)³⁺¹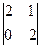=4-0=4

A₃₂=(-1)³⁺²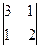=-(6-1)=-5

A₃₃=(-1)³⁺³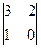=0-2=-2

3) Енді кері матрицаны табайық:

A^-1==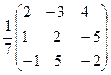

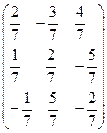
Тексеру AA^-1=Е

Сонда, AA^-1===

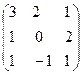
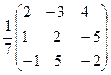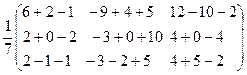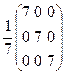===E Жауабы: A^-1=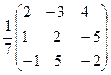

Матрицаның рангісі.

Анықтама. А матрицаның нөлге тең емес минорының ең жоғарғы реті оның рангісі деп аталады және ол rang А деп белгіленеді.

Элементтер түрлендірулер матрицаның рангісін өзгертпейді. Элементар түрлендірулер деп мына түрлендірулерді айтамыз:

1) Транспонирлеу – матрицаның барлық тік жолдарын сәйкес жатық жолдарымен орын ауыстыру;

2) Екі тік (жатық) жолдын орын ауыстыру;

3) Кез келген тік (жатық) элементтерін 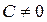санына көбейту;

4) Кез келген тік (жатық) жолының элементтерін 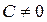санына көбейтіп келесі кез келген тік (жатық) жолының сәйкес элементтеріне қосу.

m*n-ретті А матрицасын қарастырайық:

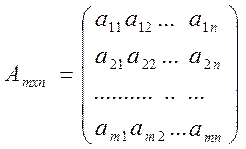
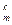
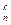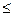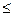Берілген m*n-ретті матрицадан k-ретті СCминор құруға болады, мұндағы kn, km (C=)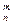

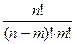Мысалы, 3*4 ретті

A=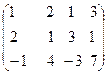

матрицадан бірінші ретті (k=1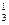) CC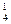=12 минор құруға болады. Ол минорлар берілген матрицаның элементтері. Ал екінші ретті (k=2) 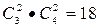минор құруға болады. Берілген матрицаның нөльден өзгеше екінші дәрежелі миноры бар болады.

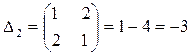
Үшінші ретті минорлар (k=3) 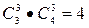минор құруға болады. Үшінші ретті минорлардың барлығы да нөльге тең:

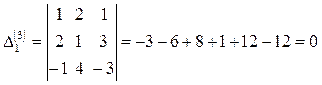
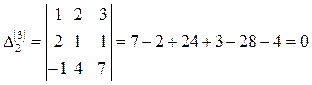
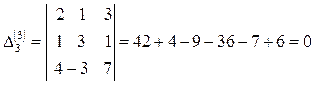
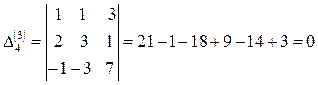
Алынған матрицаның реттілігі бұдан жоғары минорлары болмайды. Олай болса, бұл матрицаның рангісі rang A=2. Енді осы есепті екінші тәсілмен табайық, элементар түрлендіру әдіспен:

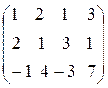
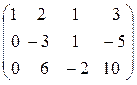
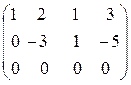
Сонымен, r=rang A=2. [kgl]