Миноры матрицы

Пусть в матрице 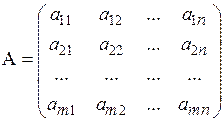выделены
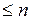какие-либо k строк и k столбцов, k и k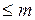. Элементы, расположенные на пересечении этих строк и столбцов, образуют квадратную матрицу А¢ порядка k (подматрицу матрицы А).
Ее определитель 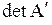называется минором k-го порядка данной матрицы А. Очевидно, что в общем случае таких миноров матрицы А может быть несколько. При этом максимальный порядок миноров равен минимальному из чисел m и n, т.е. 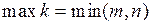. Из всех возможных миноров матрицы А выделим те, которые отличны от нуля. В свою очередь, среди этих миноров можно найти по крайней мере один минор наибольшего порядка.

Определение. Наибольший порядок минора, отличного от нуля, называется рангом матрицы.

Определение. Отличный от нуля минор матрицы, порядок которого равен рангу матрицы, называется базисным минором этой матрицы.

Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными.

В общем случае у матрицы может быть несколько базисных миноров.

Важную роль играет следующая основная теорема, которую мы приводим без доказательства.

Теорема 3.6. (о базисном миноре). Базисные строки (базисные столбцы) матрицы линейно независимы. Любая строка (любой столбец) матрицы А является линейной комбинацией базисных строк (базисных столбцов).

Таким образом, если ранг матрицы А равен r, то в этой матрице обязательно имеется минор r -го порядка, отличный от нуля, а все миноры, порядок которых больше r, равны нулю.

Ранее было дано определение ранга матрицы как наибольшего числа линейно независимых ее вектор-строк (столбцов). В курсе алгебры доказывается, что эти два определения эквивалентны. Это дает возможность вычислять ранг матрицы, а значит, и ранг системы векторов.

Пример. Найти все базисные миноры матрицы

А=.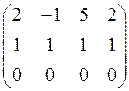

○ Любой минор матрицы А третьего порядка равен нулю, так как содержит нулевую строку. Будем находить миноры второго порядка, отличные от нуля.

, , , , .

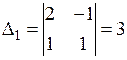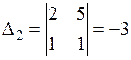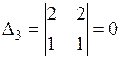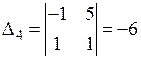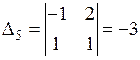Среди миноров второго порядка есть отличные от нуля, значит ранг матрицы А равен 2 и базисными минорами являются . ●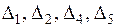

Теорема 3.7. Для того чтобы определитель 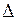n-го порядка был равен нулю, необходимо и достаточно, чтобы его строки (столбцы) были линейно зависимы.

□ 1) Пусть определитель квадратной матрицы А порядка n равен нулю. Тогда максимальный порядок миноров, не равных нулю, должен быть меньше n; следовательно, ранг матрицы А меньше n. Это означает, что система всех строк матрицы линейно зависима.

2) Если строки А¹, А²,…, А^mопределителя 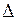линейно зависимы,
то по свойству 6° линейной зависимости одна строка А ⁱ является линейной комбинацией остальных строк определителя, т.е.

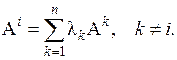Прибавив к строке А ⁱ эту линейную комбинацию, умноженную на (–1), получим одну строку, целиком состоящую из нулей, при этом на основании свойства 7° определителя величина определителя 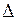не изменится. Но тогда по свойству 2° определитель равен нулю. ■

Пример. Доказать, что векторы a ₁=(2;–1;3), a ₂=(–1;1;0), a ₃=(1;1;6) компланарны.

○ Три ненулевые трехмерные векторы компланарны, если они линейно зависимы. Составим определитель из координат этих векторов

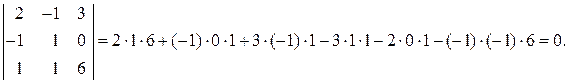
Так как определитель равен нулю, то его строки линейно зависимы, значит, линейно зависимы векторы a ₁=(2;–1;3), a ₂=(–1;1;0), a ₃=(1;1;6), следовательно, они компланарны. ●