Свойства ранга матрицы

1°. Ранг матрицы не изменится, если к этой матрице приписать строку, являющуюся линейной комбинацией других строк матрицы.

□ Пусть ранг матрицы А с размерами 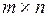равен r. Значит, среди строк матрицы А ровно r линейно независимых. Для определенности будем полагать, что это первые r строк 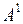,,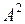…,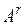. Тогда остальные строки линейно выражаются через 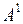,,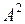…,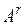. Припишем к матрице А строку, являющуюся линейной комбинацией строк матрицы А. В полученной матрице 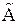размера 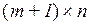все строки, в том числе и приписанная, линейно выражаются через 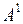,,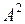…,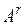. Следовательно, ранг матрицы 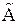также равен r. ■

Следствие. Ранг матрицы не изменится, если вычеркнуть из этой матрицы строку, являющуюся линейной комбинацией остальных строк матрицы.

□ Действительно, если обозначить исходную матрицу через 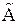, а матрицу, полученную из нее вычеркиванием строки, являющейся линейной комбинацией остальных строк матрицы, через А, то окажется, что 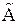можно получить из А добавлением строки, являющейся линейной комбинацией строк из А. Но в таком случае, согласно свойству 1°, ранги матрицы А и 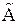должны быть равны. ■

2°. Ранг матрицы не изменится, если к одной из ее строк прибавить линейную комбинацию других строк матрицы.

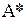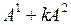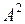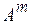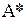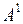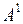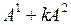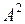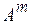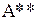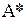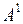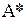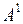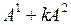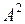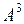□ Добавим, например, к первой строке матрицы А вторую строку, умноженную на некоторое число k. В результате получим матрицу , строки которой ,,…,. Припишем к матрице в качестве новой строки , получим матрицу со строками ,,,…,, при этом r ()= r () (по свойству 1°), так как есть линейная комбинация строк матрицы : =()– k +0×+…+0×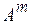. В матрице 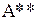вторая строка 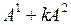является линейной комбинацией остальных строк этой матрицы, а значит ранг матрицы 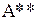не изменится, если из нее вычеркнуть вторую строку. В результате получим матрицу со строками 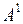,,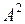…,,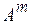 т.е. исходную матрицу А. Следовательно, r (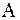)= r (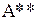)= r (). ■

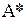3°. Ранг матрицы А не изменится, если к этой матрице приписать нулевую строку.

□ Нулевую строку всегда можно рассматривать как линейную комбинацию строк матрицы А: 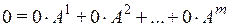, поэтому свойство 3° следует из свойства 1°. ■

Следствие. Ранг матрицы А не изменится, если вычеркнуть из этой матрицы нулевую строку (конечно, при условии, что такая строка имеется).

Замечание. Рассмотренные свойства ранга справедливы и для столбцов матрицы.