Расчет отданной (воспринятой) телом теплоты

Количество теплоты Qt (Дж), отданной (воспринятой) телом за время t в процессе охлаждения (нагревания), равно: ,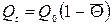

где 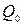- количество теплоты, переданной за время полного охлаждения (нагревания), (Дж); 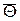- средняя по объему безразмерная температура тела в момент времени t. Для пластины толщиной 2δ и площадью поверхности А теплота, переданная за время полного охлаждения, равна: 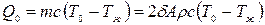, где 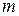- масса пластины, кг; 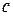- теплоемкость материала пластины, 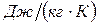; 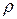- плотность, 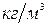. Средняя по объему безразмерная температура пластины в момент времени t при :

. (**)

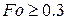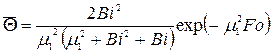Для параллелепипеда со сторонами 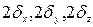теплота, отданная за время полного охлаждения, равна: .

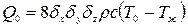Средняя по объему безразмерная температура параллелепипеда:

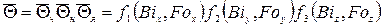
где 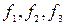определяются по справочным данным. Если 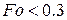, то для вычисления используется ряд, члены которого определяются по формулам типа (**).

Методы решения задач нестационарной теплопроводности

Как было показано, для решения уравнений нестационарной теплопроводности вводят понятие безразмерной температуры тела Θ, чисел Био 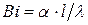, Фурье 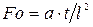и безразмерных координат, обозначаемой для пластины 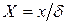, а для цилиндра 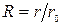.Определение температуры тела производят с помощью полученных аналитически выражений через соответствующие значения коэффициентов, например P, N, μ1 μ12, определяемые как f(Bi) по справочным таблицам и графикам.

Однако предлагаемый метод имеет ограничения по расчетной области, связанный с конечным набором коэффициентов и граничными условиями.

В связи с этим для решения задач нестационарной теплопроводности применяют численные методы. Например, метод конечных разностей (сеток). При численном решении таким методом могут быть получены значения температур на некотором конечном множестве точек, называемой сеткой.

Процедура численного решения начинается с замены исходного дифференциального уравнения теплопроводности его конечно-разностным аналогом. Для численного решения задач нестационарной теплопроводности могут быть использованы разностные уравнения, составлены по явной или неявной схемам.

Явные конечно-разностные уравнения. При решении одномерного уравнения теплопроводности 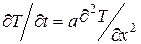его конечно-разностный аналог запишется в виде: 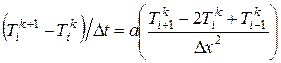. Здесь 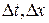- шаг по времени и координате; 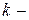момент времени; 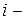номер узла разностной сетки; 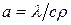– коэффициент температуропроводности.

Разрешая уравнение в явном виде относительно неизвестной функции 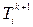, получаем: 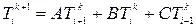, где 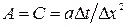, 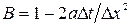; 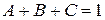. Для того, чтобы исключить неограниченный рост 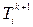в процессе расчета, необходимо выполнять условие устойчивости системы разностных уравнени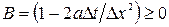й: или 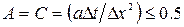; максимально допустимое значение шага по времени: 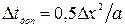.Соответственной говорят, что явная схема использует разность по времени вперед, а неявная по времени назад относительно момента времени, для которых составлены пространственные разности.

Неявные конечно-разностные уравнения. В этом случае конечно-разностный аналог запишется в виде: .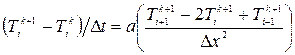

Разрешая уравнение в неявном виде относительно неизвестной функции 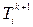, получаем: .

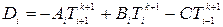Решение уравнения сводится к необходимости отыскания значение коэффициентов 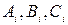, 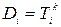. Методика решения сводится к массиву линейны уравнений и решение их методом «прогонки».