Операции над множествами

Для визуализации отношений между множествами и операций над множествами обычно используются диаграммы Эйлера-Венна, на которых представлены результаты операций над множествами точек как над геометрическими фигурами на плоскости. Универсальное множество обычно обозначают графически в виде множества точек прямоугольника, а отдельные множества в виде отдельных областей (кругов или овалов) внутри этого прямоугольника.

Определение 1: Объединением (или суммой) двух множеств А и В называется новое множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств, то есть или А, или В:

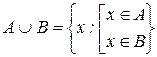По аналогии с алгеброй чисел объединение иногда называют суммой множеств, так как операция объединения множеств обладает многими свойствами операции сложения чисел.

Определение 2: Пересечением (или произведением) двух множеств А и В называется новое множество, состоящее из элементов, каждый из которых принадлежит обоим этим множествам, то есть и А, и В:

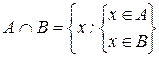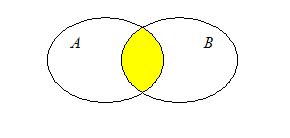По аналогии с алгеброй чисел пересечение иногда называют произведением множеств, так как операция пересечения множеств обладает многими свойствами операции умножения чисел.

Определение 3: Разностью двух множеств А и В называется новое множество, состоящее из элементов, каждый из которых принадлежит множеству А, но не принадлежит множеству В:

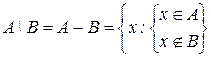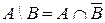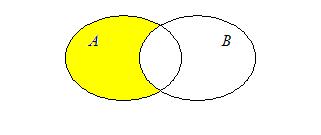Множество А\В называется также дополнением множества В относительно множества А.

Определение 4: Если U – универсальное множество и А Ì U, то разность U\A называется дополнением множества А до множества U, или просто дополнением множества А и обозначается Ā:

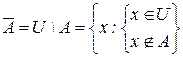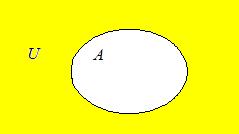Определение 5: Симметрической разностью двух множеств А и В называется новое множество, обозначаемое А D В и состоящее из тех и только из тех элементов, которые принадлежат А \ В или В \ А:

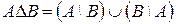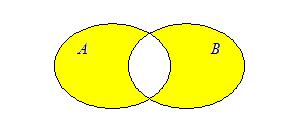Пример:

Выписать все подмножества трёхэлементного множества М ={ а, b, c }.

{ а, b, c }

{ а, b } { а, c } { b, c }

{ а } { b } { c }

Определение 6: Алгебра множеств — это непустая система подмножеств (некоторого множества U), замкнутая относительно операций объединения, пересечения, дополнения и симметрической разности.

Например, алгебра натуральных чисел незамкнута относительно вычитания.

В теории алгебры множеств множестваÆ и U играют такую же роль, что и числа 0 и 1 в теории алгебры чисел.

Основные свойства алгебры множеств:

Закон	Объединение È	Пересечение Ç	Разность \	Симметрическая разность D
Коммутативность (переместительный)	А È В = В È А	А Ç В = В Ç А	¾	А D В = В D А
Ассоциативность (сочетательный)	(А È В)È С = А È(В È С)	(А Ç В)Ç С = А Ç(В Ç С)	¾	(А D В)D С = А D(В D С)
Дистрибутивность (распределительный)	(А Ç В)È С =(А Ç С)È(В Ç С)	(А È В)Ç С =(А È С)Ç(В È С)	¾	¾
Дистрибутивность (распределительный)	(А \ В)È С =(А \ С)È(В \ С)	(А \ В)Ç С =(А \ С)Ç(В \ С)	¾	¾
Поглощения	(А Ç В)È А = А	(А È В)Ç А = А	¾	¾
Склеивания (исключения)	(А Ç В)È(Ā Ç В)= В	(А È В)Ç(Ā È В)= В	¾	¾
Идемпотентность (отсутствие показателей степени)	А È А = А	А Ç А = А	А \ А =Æ	А D А =Æ
Исключения третьего и противоречия	А È Ā = U	А Ç Ā =Æ	А \ Ā = А	А D Ā = U
	¾	¾	Ā \ А = Ā	¾
законы, связывающие пустое и универсальное множества	А ÈÆ= А	А ÇÆ=Æ	А \Æ= А	А DÆ= А
¾	¾	Æ\ А =Æ	¾
А È U = U	А Ç U = А	А \ U =Æ	А D U = Ā
¾	¾	U \ А = Ā	¾
U ÈÆ= U	U ÇÆ=Æ	U \Æ= U	U DÆ= U
¾	¾	Æ\ U =Æ	¾
Законы де Моргана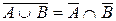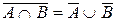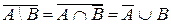
	¾	¾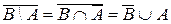
Инвальтивность (двойное отрицание)	¾	¾		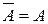¾