Метод наименьших квадратов. Классический метод Рунге-Кутта

Классический метод Рунге-Кутта

Метод Рунге-Кутта четвертого порядка получаем при

P=4, c₁=0, c₂= c₃=1/2, c₄=1, d₁=d₄=1/6, d₂=d₃=1/3

Расчетные формулы имеют вид:

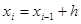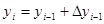; (i=1, 2, …, m) (9)

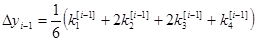
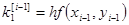
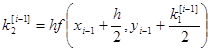
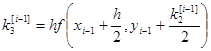
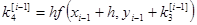
То есть берутся 4 направления и усредняются.

Для практической реализации погрешности решения можно применять правило Рунге, полагая P =4: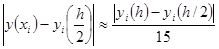

Программа решения дифференциального уравнения методом Рунге-Кутта:

program RungeKutta; {*** Mетод Рунге - Кутта ***}

var d,x,a,b,h,y,k1,k2,k3,k4:real;

m,i:integer;

function f(x,y: real): real;

begin f:=cos(x);

end;

BEGIN writeln('Введите значения концов отрезка [a,b]');

readln(a,b);

writeln('Введите начальное значение y0=y(x0)');readln(y);

writeln('Введите число значений функции на промежутке [a,b]');

read(m);

x:=a; h:=(b-a)/m;

for i:=0 to m do

begin writeln (x:10:3, y:15:4);

k1:=h*f(x,y);

k2:=h*f(x+h/2,y+k1/2);

k3:=h*f(x+h/2,y+k2/2);

k4:=h*f(x+h,y+k3);

d:=(k1+k2*2+k3*2+k4)/6; y:=y+d; x:=x+h

end; readln;

END.

Введите значения концов отрезка [a,b]

0 1.57

Введите начальное значение y0=y(x0)

Введите число значений функции на промежутке [a,b]

0.000 0.0000

0.157 0.1564

0.314 0.3089

0.471 0.4538

0.628 0.5875

0.785 0.7068

0.942 0.8087

1.099 0.8908

1.256 0.9509

1.413 0.9876

1.570 1.0000