Постановка задачи. Пусть данные некоторого эксперимента представлены в виде таблицы: xi x1 x2 xn yi y1 y2

Пусть данные некоторого эксперимента представлены в виде таблицы:

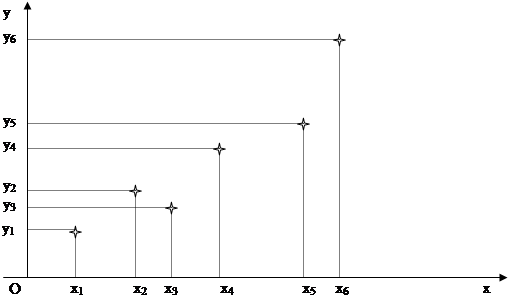
Поставим задачу об отыскании аналитической зависимости между x и y, т.е. некоторой формулы y=f(x). При этом потребуем, чтобы график искомой функции изменялся плавно и не слишком уклонялся от экспериментальных данных. Поиск такой зависимости называют «сглаживанием» экспериментальных данных. Формулу y=F(x) – эмпирической формулой или уравнением регрессии y на x.

Предположим, что приближающая функция y=F(x) имеет значения.

xi	x1	x2	…	xn
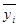
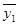
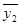
			…		(2)

Рассматривая совокупности (1) и (2) как координаты двух точек
n-мерного пространства, найдем расстояние между ними по евклидовой метрике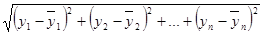

Потребуем, чтобы эта величина была наименьшей. Это равносильно тому, что сумма квадратов должна быть наименьшей:

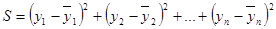или

Тогда задача приближения функции f формулируется следующим образом: для функции f, заданной таблицей, найти функцию F определенного вида так, чтобы сумма квадратов была наименьшей.