2014-02-02
920
Точечное оценивание параметров распределений СВ-н
Пусть наблюдается СВ Х с ФР F(x) и ПР р(х). Случайная выборка измерения представлена вектором Xn=(X1, …, Xn) с реализацией хn=(х1, …, хn). Будем предполагать, что законы распределения элементов выборки Хi совпадают с законом распределения наблюдаемой СВ, а закон распределения случайной вектора Xn=(X1, …, Xn) может быть найден по формулам теории вероятностей.
Параметром распределения СВ назовем ее числовую характеристику (МО, Д, момент и т.п.) либо неизвестную константу, которая явно содержится в выражении функции распределения.
Параметр распределения будем обозначать u, имея в виду, что в общем случае это векторная величина с компонентами u1, …, ur.Введем СВ 
=g(Xn) с реализацией 
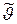=g(хn), где g – борелевская функция. Эту функцию назовем статистикой. В общем случае статистика - векторная СВ с компонентами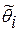 
= gi(Xn) и их реализацией 
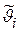=gi(хn).
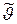Статистику , реализация которой принимается в качестве приближенного экспериментального значения параметра u, будем называть точечной оценкой этого параметра.
Ясно, что не всякая зависимость gi(Xn) может давать удовлетворительную оценку неизвестного параметра u; чтобы быть подходящей, gi(Xn) должна обладать определенными свойствами. Именно, в соответствии с принципом оптимальности добиваются, чтобы оценка = g(Xn) удовлетворяла следующим критериям точечного оценивания: состоятельность, несмещенность, эффективность, достаточность и робастность. Если все эти свойства обеспечить не удается, тоограничиваются удовлетворением хотя бы какой-то их части.
Состоятельность оценки – это сходимость ее по вероятности к оцениваемому параметру при n® ¥.
В случае состоятельной оценки вероятность сколь-нибудь существенного отличия от u мала при достаточно большом объеме выборки измерений Х. Поскольку сходимость по вероятности следует из сходимости почти наверное и в среднем квадратическом, то сходимости последнего вида также следует считать признаком состоятельности оценки . В этом случае говорят о сильной состоятельности.
Несмещенность оценки – это свойство вида: М()=u.
Несмещенность гарантирует совпадаение центра рассеяния возможных реализаций 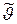с оцениваемым параметром u. Если это свойство не выполняется, т.е.
М() - u = b(u) ¹ 0, то оценку называют смещенной, при этом величину b(u) называют систематической ошибкой (смещением) оценки . Очевидно, что b(u) зависит от n. Если b(u) ® 0 при n® ¥, то оценку называют асимптотически несмещенной. Не следует абсолютизировать это свойство. Во-первых, несмещенной оценки может не быть; во-вторых, требование несмещенности может придти в противоречие с требованием минимума рассеяния относительно u.
Оценку называют эффективной, если ей соответствует минимальное значение ошибки.
В классе несмещенных оценок этот критерий означает минимальность дисперсии D(). Оценку называют асимптотически эффективной, если свойство минимальности относительно достигается в пределе n® ¥.
Оценку называют достаточной, если она содержит в себе столько же информации о параметре u, сколько её в выборке Xn=(X1, …, Xn).
Оценку называют робастной, если она в каком-то смысле слабо зависит от изменения выборки Xn=(X1, …, Xn).
Введенные признаки оптимизации оценок относятся к фиксированному состоянию параметра u. Если они имеют место для всякого u из области его возможных реализаций, то говорят о равномерной состоятельности, несмещенности, эффективности, достаточности и робастности оценки .
Оценки параметров распределений, удовлетворяющих хотя бы одному из перечисленных критериев оптимальности, могут строиться по разному.
Основная задача теории точечного оценивания состоит в разработке методов построения оценок, обладающих всеми или какими-то из перечисленных оптимальных свойств.
