2014-02-02
360
Одним из наиболее важных методов построения оценок параметров, обладающих определенными оптимальными свойствами, является метод максимума правдоподобия.
Он опирается на принцип оптимальности в виде максимума правдоподобия, когда принимается, что в опыте реализуется наиболее вероятное (соответствующее максимуму плотности вероятности или функции вероятности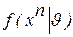 
) состояние хn выборки наблюдений Хn. В качестве оценки максимального правдоподобия (ОМП) принимается СВ 
= 
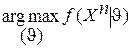и ее реализация u=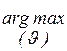
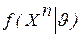. Обычно функцию 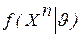, где u-переменная, а Хn – фиксированный параметр, обозначают символом 
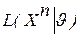и условие для определения ОМП записывают в виде: 
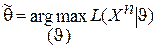. Удобнее в этом методе использовать 
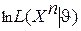и условие для определения 
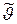записывается в виде: 
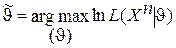. Если 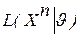дифференцируема по u и максимум 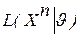реализуется как стационарная точка этой функции по переменной u, то 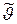находится из уравнения: 
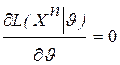или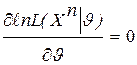 
.(*)
В случае векторного параметра u=(u1, …, ur) ОМП находится в виде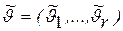 
, в частности из уравнения: 
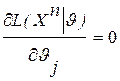или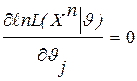 
(j=1,r) (**).
Принято называть: 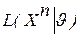- функцией правдоподобия; 
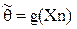– ОМП; а уравнения (*) и (**) – уравнениями правдоподобия.
