Описание ящика Эджворта

Рассмотрим простейшую модель обмена. Участников обмена двое и товаров, которыми они об­мениваются, тоже два. Первый участник, как и второй, имеет обоих товаров в каком-то количестве (возможно, что даже в нулевом). Функции полезностей участников 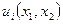, 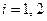. Напомним, что участники хотят обмениваться товарами, в надежде улучшить свое благосостояние. На невы­годный для себя вариант обмена они не пойдут.

Но могут ли участники обмена улучшить свое благосостояние в ре­зультате обмена?

Весьма удобной моделью исследования таких обменов в рассматриваемом простейшем вари­анте (два участника и два вида товаров) является ящик Эджворта. Опишем его.

Обозначим 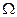, суммарное количество i-го товара у обоих участников. Пусть 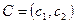– начальное, до обмена, количество товаров у первого, тогда у вто­рого их будет . Рассмотрим пря­моугольник на плоскости, одна точка которого есть 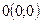, а другая – по диагонали – 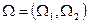, остальные две точки прямоугольника имеют коорди­наты 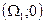и 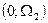. Предполагается, что обе функ­ции полезности являются строго вогнутыми, а также дифференцируемыми. Это делает выводы более чет­кими.

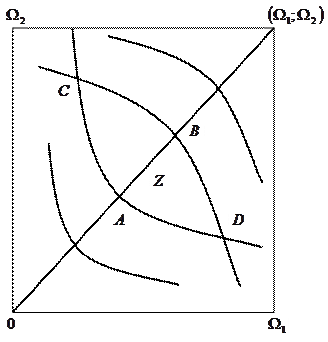
Наложим теперь на ящик Эджворта карты пред­почтений первого (относительно точки 0) и второго (относительно точки 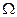). На рисунке нанесены две кривые безразличия первого – линии уровня его функции полезности 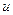– ближайшие к точке 0, и две линии безразличия второго – ближайшие к точке 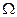. Две из этих кривых проходят через точку C – кривая CAD для первого и кривая CBD для второго. Вправо и вверх от кривой CAD расположено множе­ство предпочтительности первого 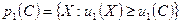, влево и вниз от кривой CBD распо­ложено множество предпочтительности второго .

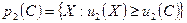Рассмотрим любую точку в «линзе» CABD. Легко видеть, что 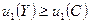и 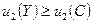, т.е. любая точка «линзы», лежащая строго внутри нее, т.е. не лежащая на кривых CAD и CBD, строго лучше точки C для каждого участника. Следовательно, оба участника вполне согласятся «перейти» в точку 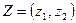, т.е. согласятся на обмен: первый отдаст второму 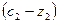единиц второго товара и получит взамен 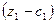единиц первого товара. Но остановятся ли на этом участ­ники? Не найдут ли они еще более хороший вариант обмена?