Равновесие на рынке. Теорема Дебре

Предположим рассмотрение этой модели. Мы уже изучали спрос потребителя, зависящий от цен 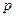и дохода 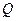. В данной ситуации доход 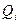, которым располагает і-й участник, есть 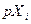_, тем самым его спрос 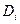есть фактически функция цен, которые могут быть пока неизвестны. Вектор суммарного спроса также есть функция цен 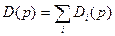. В тоже время предположение това­ров фиксировано, ибо весь запас 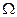находится на руках у участников экономики и равен .

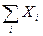Введем в рассмотрение вектор-функцию избыточного спроса 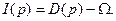. Ясно, что ком­понента 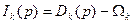представляет собой превышение спроса на k-й товар на всем рынке 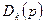над предложением 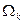и равенство спроса и предложения на всем рынке, т.е. равновесие на рынке выражается равенством 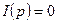или 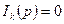для всякого .

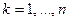Определение. Если вектор цен 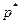удовлетворяет равенству 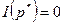, то он называется системой равновесных цен, а вектор 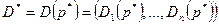– равновесным распреде­лением.

Итак, в ситуации равновесия суммарный спрос на каждый товар в точности равен предложению этого товара: для каждого .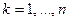

Но при каких же условиях существуют ситуации равновесия? Первыми решили эту проблему А. Вальд в 1933-1936 гг. и Дж. Фон Нейман в 1937 г. Но еще в 1874 г. Л. Вальрас несколько упро­стил задачу, сведя ее к решению нескольких обычных уравнений, причем число уравнений и число неизвестных оказалось одинаковым. Он же открыл закон, относящийся к рассматриваемой ситуации и носящий сейчас его имя.

Предложение. Функция избыточного спроса удовлетворяет закону Вальраса .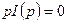

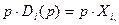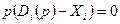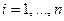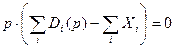Действительно, значит для каждого . Складывая эти равенства, получим , и, окончательно, , т.е. .

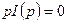Заметим теперь следующее. Как известно, функция спроса зависит только от соотношения цен, а не от их абсолютных значений. Это замечание позволяет ввести в рассмотрение и деньги как не­который особый, но, в общем-то, такой же товар, как и остальные.

Применяя закон Вальраса, получаем, что имеющиеся на руках количество денег равно 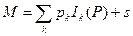, где 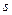– спрос на деньги. В частности, если спрос 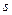равен нулю, т.е. никто не хочет иметь деньги для их хранения или еще для чего-нибудь долговременного, например, для трат вне рынка, то стоимость неудовлетворенного спроса в точности равна количеству денег на руках у участников рынка. Это и есть ситуация равновесия. Представьте, что вдруг «мешок» денег пропал («челнок» по рассеянности засунул его куда-то в своей палатке). Немедленно станет ощу­щаться дефицит денег, и их «цена» возрастет, т.е. упадут остальные цены.

Продолжим. В общем случае доказательство существования ситуации равновесия довольно трудно и использует весьма сложные математические понятия. Сформулируем без доказательства теорему о равновесии, принадлежащую Дебре.

Теорема 3. Если системы предпочтений участников непрерывны, строго выпуклы и в начале каждый участник обладает всеми товарами (хотя бы в небольших количествах), то существует си­туация равновесия, т.е. система равновесных цен и равновесное распределение.

Доказывается также, что и любое равновесное распределение оптимальное по Парето и не бло­кирующееся никакой коалицией, т. е. принадлежащее ядру экономики.