Множество распределений, оптимальных по Парето

Итак, как уже стало ясно, любое распределение товаров в количестве 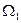первого товара и 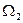– второго между участниками соответствует некоторой точке 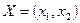в ящике Эджворта: 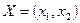единиц у первого, а остальное, т.е. – у второго. Специально для этой ситуации конкретизируем общее понятие оптимальности по Парето.

Распределение 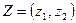называется оптимальным по Парето, если не существует распределе­ния 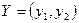, такого, что 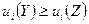, 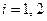и хотя бы для одного из участников .

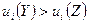Назовем 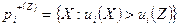множеством строгой предпочтительности i-го участника. Ясно, что 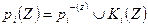, где 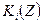– кривая безразличия i-го участника, проходящая через точку 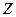. Скажем, что кривые безразличия 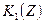и 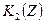касаются, если существует прямая, прохо­дящая через точку 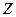и разделяющая множества 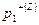и .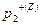

Предложение 1. Распределение 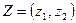является оптимальным по Парето, если и только если в этой точке кривые безразличия 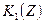и 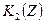касаются.

Предположение о строгой вогнутости функций полезности влечет строгую выпуклость мно­жеств 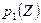и 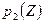, в силу чего оказывается справедливым следующее предложение.

Предложение 2. Распределение 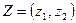является оптимальным по Парето, если и только если множества строгой предпочтительност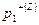и и 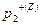не пересекаются.

Доказательства обоих предложений несложны.

Если функции полезности 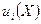, 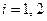дифференцируемы, то введенное только что понятие ка­сания кривых безразличия совпадает с обычным понятием касания кривых, как имеющих об­щую касательную.