2014-02-02
262
Как и в предыдущей модели, общие ресурсы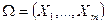 
с самого начала распределены между 
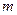участниками. Но, кроме того, имеем 
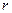производственных единиц, каждая из которых характеризуется производственным множеством 
, 
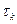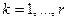. Глобальное производственное множество задается равенством 
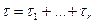. При этом каждый производитель руководствуется двумя правилами:
1. Правило управления: производитель максимизирует свою прибыль, т.е. в ответ на систему цен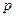 
он выбирает вектор 
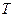, максимизирующий прибыль 
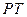, где 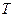– выбранная им технология;
2. Правило распределения прибыли: реализованная прибыль распределяется между участниками согласно фиксированным заранее коэффициентам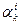 
– доля i-го участника в прибылях k-го производителя; конечно, 
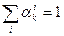для каждого 
.
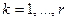Видно, что участники являются акционерами, а производитель не является, вообще говоря, каким-то конкретным участником. Это будет так, если все коэффициенты 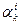для данного производителя равны нулю, кроме какого-нибудь одного, например 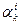= 1; тогда j-й участник есть владелец k-го производства.
Итак, производители имеют свои собственные правила работы, которые предполагают знание системы цен на рынке, но не предполагают знание системы предпочтений других участников экономики.
Для i-го участника денежная сумма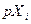 
являющаяся оценкой его начальных запасов товаров, пополняется дивидендами, получаемыми от разных производственных единиц, и в целом составит 
.
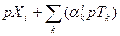Итак, каждый производитель максимизирует свою прибыль и отдает дивиденды акционерам; потребитель покупает то, что он предпочитает, и столько, за сколько он в состоянии заплатить.
В рассматриваемой модели также можно определить, что такое равновесное состояние, равновесные цены и доказать теорему о существовании равновесия. Однако эта теорема не гарантирует однозначность в действиях производителей и потребителей, что может привести к своеобразному дисбалансу действий участников экономики.
Лекция 14. Ящик Эджворта
1. Описание ящика Эджворта.
2. Множество распределений, оптимальных по Парето.
3. Равновесные распределения.
