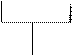
Выберем в качестве структурной схемы автомата схему вида [7]:
z(t)

 p1
p1





 der r
der r
p2 Дешифр. Комб. z(t+1) Рег. 1 Рег. 2



 xi схема derr
xi схема derr

 p3 dok dok
p3 dok dok





t1 t2
НУ
Схема состоит из комбинационной схемы, реализующей функцию возбуждения элементов памяти, дешифратора и регистров 1 и 2. Регистры это элементы памяти, построенные на основе триггеров. При синхронной реализации автомата полагается, что все переходные процессы в схеме успевают закончиться к моменту прихода сигнала t1, стробирующего (разрешающего) прием информации с выходов комбинационной схемы в триггеры регистра 1. Второй триггерный регистр, прием информации в который стробируется синхросигналом t2, нужен для того, чтобы все состояния автомата сделать устойчивыми. Триггеры регистра 1 будем называть вспомогательными, а регистра 2 - основными. В схеме обязательно формирование сигналов derr - сигнала ошибки и dok - сигнала принадлежности входной цепочки символов языку заданной грамматики.
Комбинационная схема вместе с формированием сигналов derr и dok формирует сигналы вектора z(t+1). z(t+1) есть состояния элементов памяти в момент времени t+1. Они учитывают сигналы на входе автомата xi и состояния элементов памяти в предыдущий момент времени t. Все это осуществляется на основе алгоритма построения переключательных функций элементов памяти для заданной грамматики.
С помощью сигнала НУ осуществляется начальная установка триггеров автомата. Пусть входные символы xi представляются двоичными кодами с переменными кода pj. Любая входная цепочка должна заканчиваться маркером или символом «конец цепочки», чтобы автомат мог различать конец обработанной цепочки и начало следующей. В структурную схему автомата часто вводится дешифратор, назначение которого преобразовывать двоичный код, состоящий из символов pi в унитарный код, состоящий только из одной переменной xi, то есть когда только одна из выходных переменных принимает значение 1, в то время как все другие равны нулю.
Пример. Пусть имеем таблицу кодов входных символов вида:
| Символ | p1 | p2 | p3 |
| x0 | |||
| x1 | |||
| x2 | |||
| x3 | |||
| x4 | |||
| x5 | |||
| x6 | |||
| x7 |
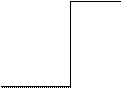
построить фрагмент схемы дешифратора для формирования сигналов x0
и Øx0.
Решение. Схема будет иметь вид:

 p1
p1







 & & x0
& & x0
 &
&

 p2
p2 


 &
&

 p3
p3

 &
&
Комбинационная схема автомата реализует функцию его переходов. Исходным заданием для ее построения является таблица или граф переходов, а также выбранный вариант кодирования. Построить функцию переходов, значит найти переключательные функции кодирующих (внутренних) переменных. Каждая внутренняя переменная z1,z2,z3,z4 представляется состоянием соответствующего элемента памяти, то есть триггера. По переключательным функциям внутренних переменных находятся функции возбуждения соответствующих им триггеров. Сложность функций возбуждения и, следовательно, сложность комбинационной схемы существенно зависит от выбора типа триггера. Реализация этих функций образует комбинационную схему автомата. В общем виде схема, реализующая переключательные функции имеет вид:
x0 x1 x2 x3 x4 x5 x6 x7 x8 z1(t) z2(t) z3(t) z4(t) t+1









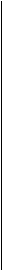









 z1 1 1
z1 1 1




 f x0 z2 2 5 1 z1(t+1)
f x0 z2 2 5 1 z1(t+1)


 z3 3 9
z3 3 9

 z4 4...
z4 4...

 z15 2
z15 2

 z26 6 1 z2(t+1)
z26 6 1 z2(t+1)





 z3 7 10
z3 7 10


 f x1 z4 8...
f x1 z4 8...



 3
3

 71z3(t+1)
71z3(t+1)



 11
11







 ...
...
 … 4 1
… 4 1


 8z4(t+1)
8z4(t+1)

...
 |
Рассмотрим построение схемы переключательной функции fx0.
 z(t)
z(t)


 f x0 z(t+1)
f x0 z(t+1)
x0
Пусть сигнал x0 обрабатывается автоматом в соответствии с таблицей переходов следующим образом: r7 ® r2; r6 ® r0. Тогда в соответствии с принятой кодировкой состояний автомата:
| r0 | |
| r1 | |
| r2 | |
| r3 | |
| r4 | |
| r5 | |
| r6 | |
| r7 | |
| r8 | |
| r9 | |
| r10 |
можно составить таблицу переходов автомата по символу x0 в кодах, будем иметь:
| t | t+1 | ||||||||
| z1 | z2 | z3 | z4 | z1 | z2 | z3 | z4 | ||
| r6 | r0 | ||||||||
| r7 | r2 |
Запишем в соответствии с последней таблицей функции z(t+1):
z1(t+1) = z1(t); z2(t+1) = z4(t);
z3(t+1) = z3(t); z4(t+1) = z4(t).
Построим схему реализации функции z(t+1) на элементах {&, Ø}:
z1 z2 z3 z4









 & & z1(t+1)
& & z1(t+1)
 |  | ||||
 |
z2(t+1)






 & &
& &
z3(t+1)






 & &
& &
 |
 z4(t+1)
z4(t+1)






 & &
& &
x0
Рассмотрим построение логической схемы переключательной функции fx1 аналогично предыдущему построению. Автомат по x1 осуществляет переходы:
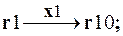
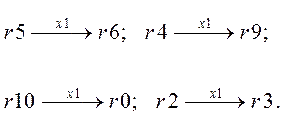

| z1(t) | z2(t) | z3(t) | z4(t) | z1(t+1) | z2(t+1) | z3(t+1) | z4(t+1) | ||
| r1 | r10 | ||||||||
| r2 | r3 | ||||||||
| r4 | r9 | ||||||||
| r5 | r6 | ||||||||
| r10 | r0 |
Построим логическую функцию для z1(t+1), пользуясь правилами построения СДНФ по таблице истинности и минимизации слабо определенной функции с использованием карт Карно. Считаем, что в пустых клетках карты Карно функция не определена.
 z1
z1




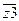 * * 0 0
* * 0 0 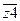
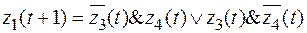 .
.
 * * 1 * z4
* * 1 * z4
 z3 0 * * *
z3 0 * * * 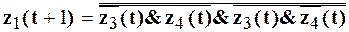 .
.
* * * 1 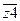
 |
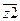 z2
z2 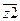
Аналогично составляются логические функции остальных zi(t+1) и строятся комбинационные схемы fxi , а в итоге общая комбинационная схема.
Построение комбинационной схемы, реализующей функцию derr
Функция возбуждения сигнала ошибки может быть представлена в виде:
derr = x0 & derrx0 Ú x1 & derr x1 Ú... Ú x8 & derr x8.
Считаем, что ошибка по xi может возникнуть тогда, когда на xi сработает какое-либо состояние, не соответствующее заданному значению по таблице переходов. Или другими словами, при приходе сигнала xi автомат находится не в тех состояниях, которые ему предписаны таблицей переходов.
Пример. Построить функцию ошибки при обработке сигнала xi.
Решение. Пусть согласно таблице переходов, рассмотренной выше, по x0
допускаются переходы: r7 ® r2; r6 ® r0.
Таким образом, можно записать:
derr Х0 = ØZ1 & Z2 & ØZ3 & ØZ4 V Z1 & ØZ2 & ØZ3 & Z4.
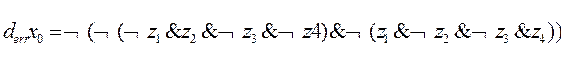 .
.
Аналогично ищутся функции ошибок для остальных xi. Составим таблицу функций ошибок, в которой показано, что ошибка будет всегда равна 1, если на xi нет переходов из обозначенных состояний, т.е. смены состояний и равна 0 в противном случае:
| ri | код | derr Х0 | Øderr Х0 | … |
| r0 | … | |||
| r1 | … | |||
| r2 | … | |||
| r3 | … | |||
| r4 | … | |||
| r5 | … | |||
| r6 | … | |||
| r7 | … | |||
| r8 | … | |||
| r9 | … | |||
| r10 | … |
Анализ таблицы показывает, что в ней единиц больше нулей. Поэтому по ней удобнее строить логическую функцию 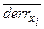 . Построение идет на основе СДНФ с минимизацией по картам Карно:
. Построение идет на основе СДНФ с минимизацией по картам Карно:
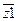 z1
z1




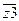 0 1 0 0
0 1 0 0 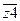
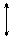 * * 0 1 z4
* * 0 1 z4
 z3 0 * 0 0
z3 0 * 0 0
0 * 0 * 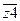

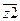 z2
z2 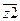
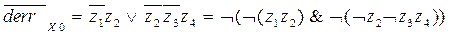 .
.
Здесь знак логического умножения опущен в слагаемых для улучшения читабельности формулы. Запишем формулу отрицания полученной функции, получим:

Аналогично определяются и остальные derr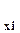 . После этого их логические схемы объединяются в одну схему. Таким образом, часть комбинационной схемы конечного автомата, отвечающая за формирование сигнала ошибки соответствует функции:
. После этого их логические схемы объединяются в одну схему. Таким образом, часть комбинационной схемы конечного автомата, отвечающая за формирование сигнала ошибки соответствует функции:
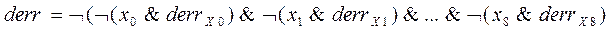
Функция ошибки для рассматриваемого примера выразится следующей комбинационной схемой:
 |



 &
&

 &
&









 & & &
& & &




 &
&




 &
&
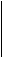


 &
&





 derr
derr

 ... &
... &

z1 z2 z3 z4 x0
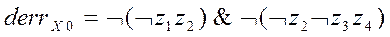 .
.
Определение функции распознавания цепочек входного языка dok
Очевидно, что сигнал dok = 1 вырабатывается только тогда, когда на вход автомата пришел сигнал конец цепочки, например, x8 и автомат находится в заключительном состоянии, то есть:
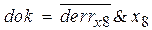 .
.
В заключение параграфа синтеза структуры автомата отметим некоторые важные моменты.
Сигнал начальной установки (НУ) устанавливает триггеры в начальное состояние, соответствующее аксиоме грамматики перед началом работы автомата или во время работы автомата, если при работе возникли некоторые технические сбои. В процессе нормальной работы автомата переход в начальное состояние осуществляется автоматически по приходу сигнала «конец цепочки».
Определим частоту тактового генератора для сигналов t2 и t1.
Периоды подачи сигналов t1 и t2 определяются в соответствии с
формулами D1 = T1 + d1, D2 = T2 + d2, где T1, Т2 - длительности
тактовых импульсов t1 и t2 соответственно, а d1, d2 - интервалы
между этими импульсами. Частота подачи сигнала определяется как
величина f = 1/D.
Поскольку триггеры регистра 2 считаются основными, то
Т2 > tмакс. + tперех. пр. 2,
где tмакс. - максимальное время, необходимое комбинационной схеме для формирования нового внутреннего состояния автомата Z(t+1) при приходе очередного входного символа xi, а также необходимое для формирования сигналов derr и dok; tперех. пр. 2 - время переходного процесса рабочей фазы триггеров регистра 2.
Во время Т2 сигналы t2 = 1, t1 = 0. Таким образом, можно записать выражение, характеризующее D2:
D2 > tмакс. + tперех. пр. 2 + d2,
где d2 - промежуток между синхросигналами t2. Отметим, что в течение времени tперех. пр. 2 происходит запись информации с регистра1 в регистр2; в течение времени tмакс работает комбинационная схема, то есть формируются сигналы Z(t+1) и сигналы derr и dok, в течение интервала d2 (t1 = 1, t2 = 0) идет запись информации в регистр1. В качестве одного из допустимых вариантов назначения периодов подачи сигналов t1 и t2 может быть рассмотрен вариант:
D1 = T1 + d1 = D2, d1 = T2, Т1 = d2,
то есть синхросигналы t1 и t2 подаются в противофазе.
 2014-02-02
2014-02-02 699
699








