Соотношение неопределенностей

Для классической механики состояние кл. частицы описывается т.н. динамическими переменными импульсом, энергией, значениями координат.

Своеобразие квантовых частиц состоит в том, что она одновременно точно не может иметь значения координаты х и компоненты импульса 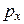. Согласно соотношению неопределенностей В. Гейзенберга, открытому в 1927 году между неопределенностями х и 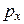существует соотношение:

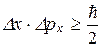
Величины 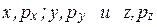называются канонически сопряженными.

(На определение энергии частицы с точностью 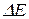требуется время не меньше )

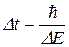Принцип неопределенности Гейзенберга:

Произведение неопределенностей двух канонически сопряженных переменных не может по рядку величины быть меньше .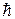

Так как 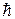очень мало (1,05 × 10^-34 Дж × с), то соотношение неопределенностей проявляет себя ярко в микромире.

Поясним соотношение неопределенностей из следующего примера. Пусть на пути частицы расположена щель 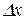- ширина щели. Определим координату х частицы. Перед щелью х – совершенно неопределенна, а .

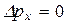При пролете через щель координата определена с точностью 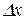, а импульс приобретает за счет дифракции электрона неопределенность 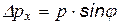. Считая для щели условие максимумов для волнового процесса с 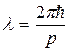, получим

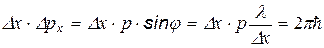
по порядку величины совпадает с .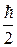

Учитывая, что 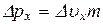из соотношения Гейзенберга

Это соотношение показывает, что чем больше m, тем меньше неопределенность x и 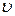, тем с большей степенью точности можно говорить о понятии траектории микрочастицы.