Квантовомеханическая модель атома водорода

Квантовая физика дает для атома водорода такое же решение для значений энергии атома, что и теория Бора, но она боле последовательна и описывает не только атом водорода.

Из уравнения Шредингера (стационарного)

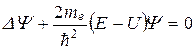
для атома водорода:

.

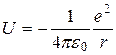Отсюда следует, что уравнение Шредингера имеет вид:

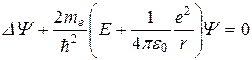(5)

Решения уравнения (5) удовлетворяют стандартным условиям в случае когда

1) Е – любое положительное значение (соответствует пролету электрона около ядра и удал в бесконечность)

2) При дискретных отрицательных значениях энергии, равной

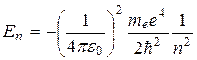, n = 1,2,3,…

Соответ. электрону, связанному с ядром.

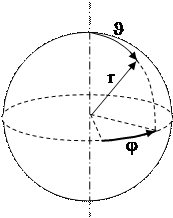
При n = 1 получим для энергии в основном состоянии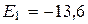эВ (энергия ионизации) так как электрон в атоме водорода движется в центрально-симметричном поле, то оператор Лапласа записывают в сферической системе координат и соответственно собственные волновые функции

,

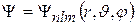которые содержат 3 целочисленных параметра n, l, m.

Число n – главное квантовое число, определяет уровни энергии

l – азимутальное или орбитальное квантовое число(определяет модуль мом. имп. )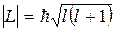

m – магнитное квантовое число (определяет проекцию мом. имп. yа некоторое напр-е z, определяемое магнитным полем )

n = 1, 2, 3,…

l = 0, 1, 2, 3, 4, (n – 1)

m = 0, ± 1, ±2, …, ±l

Энергетическое состояние электрона определяется только квантовым числом n. Решения, удовлетворяющие стандартным условиям, получаются при значениях l, не превышающих n – 1

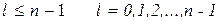- всего n значений

При данном l квантовое число m может принимать 2l + 1 различных значений

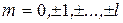
Состояния атома с одинаковой энергией (один. кв. число n), отличающиеся числами l и m, называются вырожденными состояниями.

Число различных состояний называется кратностью вырождения.

Так как для данного n 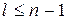, а m может принимать , значение, то кратность вырождения водородного атома:

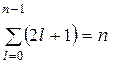
Таким образом, каждому значению E_n соответствует несколько собственных функций , отличающихся числами l и m.

Состояние электрона с l = 0 называют S – состоянием

l = 1 - P – состоянием

l = 2 - d

l = 3 - f

l = 4 - g

l = 5 - h

Так как 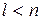, то возможны следующие состояния:

1S

2S 2P

3S 3P 3d

4S 4P 4d 4f

Еn		n	l	m		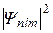состояние
Е1		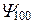				1S
Е2		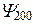				2S
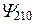					2P
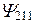					2P
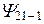			-1		2P
Е3	××××××××××××× Также как и выше для 3S и 3P
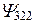					3d
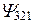					3d
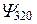					3d
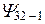			-1		3d
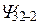			-2		3d

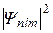- плотность вероятности

В квантовой механике доказывается, что для орбитального вантового числа имеется правило отбора

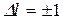
Это значит, что возможны такие переходы, при которых l изменяется на единицу.

Поэтому для серии Лаймана )

Бальмера

При увеличении числа n дискретность энергетических уровней уменьшается и характер поведения частицы приближается к классическому. В этом состоит принцип соответствия:

Принцип соответствия Бора (1923 г.):

При больших квантовых числах следствия, вытекающие из квантовой механики, должны совпадать с результатами классической теории.

Подобно тому, что при 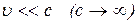релятивистская механика переходит в ньтоновскую, при 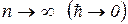квантовая механика переходит к классическому описанию. (пренебрегаем )

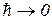Собственные функции 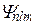распадаются на два множителя:

,

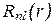- вещественный,

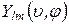- комплексный.

Так как координаты r, независимы, то при подстановке в уравнение Шредингера в сферических координатах уравнение Шредингера разбивается на две независимые части.

Первое уравнение Шредингера для радиальной части

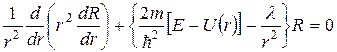
и для сферической части

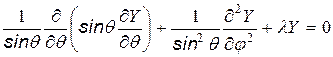
Первое уравнение зависит только от вида потенциальной энергии, а следовательно определяется конкретной физической природой взаимодействия частиц (для нашего случая – Кулоновского).

Второе уравнение не зависит от вида силового поля, поэтому его решение одинаково для всех центрально-симметричных полей.

Условие нормировки для этих уравнений имеет вид в сферических координатах:

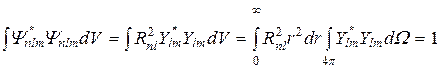
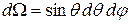- телесный угол

Из решения этих уравнений получают следующие выводы:

1) Электрон может иметь в атоме водорода лишь дискретные значения энергия:

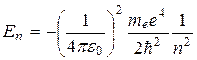, n = 1, 2, 3,…

2) Состояние электрона в атоме характеризуется набором 4 квантовых чисел

а) главного квантового числа n – определяющего энергию е.

б) орбитальное квантовое числа l – определяющего дискретное значение модуля момента импульса

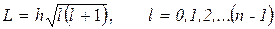
то есть для главного квантового числа m – определяющего стационарные ориентации орбитального момента электрона L в пространстве, например, их проекции на направление внешнего магнитного поля .

Диапазону значений l соответствует значений m.

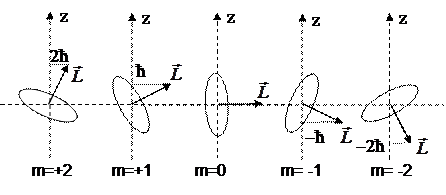Например, l = 2, то вектор момента импульса электрона в атоме может принимать в пространстве дискретных ориентаций .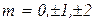

г) спинового квантового числа, определяющего ориентацию собственного момента импульса электрона (спина)

Гипотеза о существовании спина была предложена Уленбеком и Гаудсмитом (ам. ф.) в 1925 году для объяснения расщепления спектральных линий (дублеты, …, мультиплеты). Тонкая структура.

Сначала предполагалось, что электрон вращается вокруг оси, но («спин» означает «верчение»), но потом было доказано, что спин является внутренним свойством электрона (подобно массе, заряду). Спин электрона является квантовым и рел. свойством.

Собственный механический момент электрона определяется

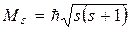
где , а проекция

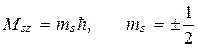
Полный механический момент электрона складывается из спинового и орбитального

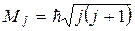
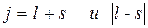
j – квантовое число полного момента импульса

Проекция полного механического момента

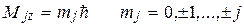
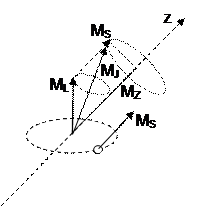Взаимодействие орбитального и магнитного момента (как взаимодействие магнитных стрелок)приводит к расщеплению энергетических уровней, а следовательно, спектральных линий. Это взаимодействие называется спин-орбитальным