2014-02-02
1177
В уравнение Шредингера 
полная энергия Е частицы входит в качестве параметра. В теории дифференциальных уравнений доказывается, что уравнения Шредингера удовлетворят стандартным условиям не при любых значениях Е, а лишь при определенных значениях, которые называются собственными значениями энергии (или др. вел.). Решения соот-е собств. зн Е называются собственными функциями. Совокупность собственных значений называется спектром. Спектр бывает дискретным и непрерывным. В случае дискретного спектра собственные значения и собственные функции можно пронумеровать
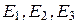
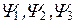
Пусть частица находится между двумя бесконечными стенками, удовлетворяющими условиям
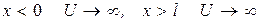
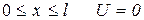
Для одномерного случая уравнение Шредингера
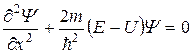
За пределами ямы вероятность обнаружения частицы равна нулю. Следовательно, и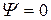 
. Из условий непрерывности на границах
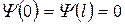
Для частицы в яме уравнение Шредингера имеет вид
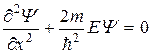
Обозначим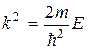 
. Для уравнения 
общим решением является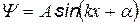 
Из условия 
Из условия 
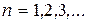
При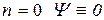 
то есть частица отсутствует.
Откуда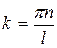 
Выразив из 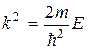энергию, получим:
 |
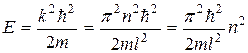
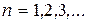
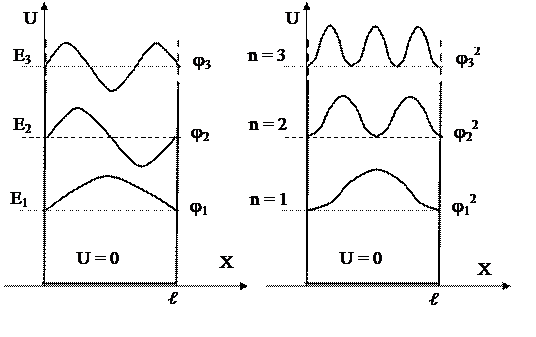Спектр энергии дискретный. Если посчитать разницу между соседними уровнями энергии и в качестве частицы взять молекулу
кг, то для ширины ямы ~ 10 см получим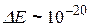 
эВ. То есть, чем больше m и больше l, тем гуще уровни энергии. Для электрона и l ~ 10-10 м (атомн. размеры) 
эВ. Найдем собственные функции
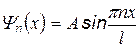
Для нахождения А воспользуемся условием нормировки
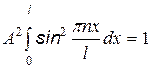
Функция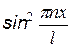 
на концах промежутка х = 0 и x = l обращается в ноль, поэтому интеграл можно получить, умножив среднее значение 
на l.
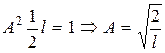
Откуда
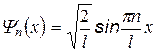
В состоянии n = z вероятность частицы нахождения посередине ямы рана 0. Классическая физика – все положения равновероятны.
ЛЕКЦИЯ № 10
