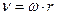 Предадим векторный вид
Предадим векторный вид 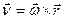 Введем радиус вектор мт… и учтем что
Введем радиус вектор мт… и учтем что 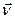 направлена по касательной окружности. По построению видно, что
направлена по касательной окружности. По построению видно, что 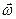 перпендикулярна плоскости окружности.
перпендикулярна плоскости окружности.
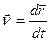
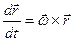
Описываем изменение во времени 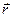 при условии что его модуль const, а конец движ. со скоростью
при условии что его модуль const, а конец движ. со скоростью 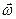 .
.
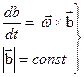
см(И3) в лекции№11
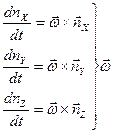
Мы переходим к случаю когда сист. отсчета НСО движется произвольно ИСО.
В общем случае это движение можно разложить на 2 состав. Первое это пост. и ускор. движ центра О-
этот случай мы рассмотрели ранее. Второе это вращательное движение сист. XOYZ с углов. скор. 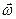 с
с
углов. ускор. 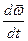 ;
; 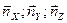 -единые орты НСО.
-единые орты НСО.
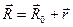 Продеференцируем по времени, один раз
Продеференцируем по времени, один раз 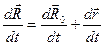
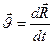 -это скорость мт в НСО.
-это скорость мт в НСО. 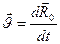 -это скорость в точке О в НСО.
-это скорость в точке О в НСО.
Найдем 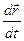 с учетом разложения
с учетом разложения 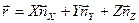 , а так же учитывая то что орты вращаются с
, а так же учитывая то что орты вращаются с
угловой скоростью 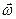 .
.
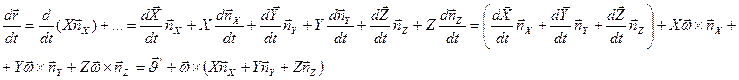
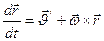 ;
; 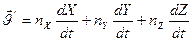
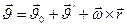 ;
; 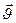 -скорость мт в НСО,
-скорость мт в НСО, 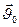 - скорость нач. координат в НСО,
- скорость нач. координат в НСО, 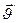 -скорость Мт в НСО,
-скорость Мт в НСО, 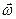 - угловая скорость вращения.
- угловая скорость вращения.
№24. Общий случай движения НСО: ускорение.
Продеференцируем обе части 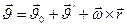 (Общий случай движения НСО: скорость.) по времени
(Общий случай движения НСО: скорость.) по времени

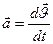 -ускорение Мт в НСО;
-ускорение Мт в НСО; 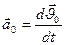 -ускорение т. О в НСО;
-ускорение т. О в НСО;
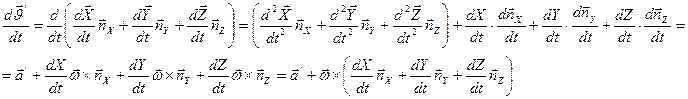
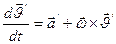 ;
; 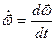 ;
; 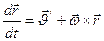 ;
;
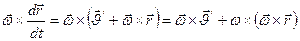
Подставим преобразования:
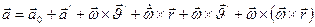
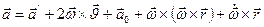 Является окончательной формулой и дает связь между
Является окончательной формулой и дает связь между 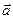
и  для произвольного движения НСО.
для произвольного движения НСО.
Вектор 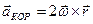 - Кориолисово ускорение.
- Кориолисово ускорение.
Введем вектор 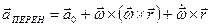 - это вектор назыв. переносным ускорением, именно такое ускор. в НСО имеет Мт, которое покоится.
- это вектор назыв. переносным ускорением, именно такое ускор. в НСО имеет Мт, которое покоится.
№25.Уравнение динами Мт в НСО.
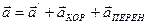 ;
; 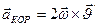 ;
; 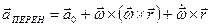 ;
;
Применим 2 з. Ньютона для ИСО в S1: 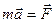 ;
; 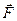 - настоящая сила.
- настоящая сила.
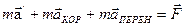 ;
;
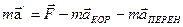 ; -Это уравнение представляет собой основной закон динамики в НСО, для общего случая поступательного и вращательного ускоренного движения относительно ИСО
; -Это уравнение представляет собой основной закон динамики в НСО, для общего случая поступательного и вращательного ускоренного движения относительно ИСО
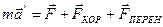
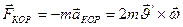 -Кореолесова сила инерции.
-Кореолесова сила инерции.
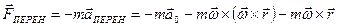
Первое слагаемое в 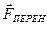 с ускорением поступательного движения системы S. Основные 2 слагаемых возникают из-за,вращательного движения НСО, с угловой скоростью
с ускорением поступательного движения системы S. Основные 2 слагаемых возникают из-за,вращательного движения НСО, с угловой скоростью 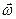 и угловым ускорением
и угловым ускорением 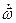 .
.
Кореолесова сила определяется с одной стороны вращением НСО, а с другой скоростью Мт относительно S.
№26. Движение Мт относительно вращающейся Земли.
 2014-02-02
2014-02-02 699
699








