2014-02-02
703
Определение 9. Отношение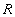 
на множестве 
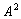называется отношением порядка, если оно обладает следующими свойствами:
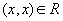для всех 
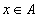(рефлексивность) - Если
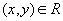и 
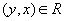, то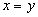 
(антисимметричность) - Если 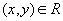и
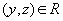, то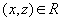 
(транзитивность)
Обычно отношение порядка обозначают знаком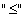 
. Если для двух элементов 
и 
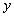выполняется 
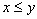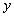, то говорят, что "предшествует" . Как и для отношения эквивалентности, условия 1-3 в таких обозначениях выглядят более естественно:
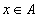для всех (рефлексивность) - Если 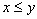и
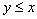, то 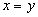(антисимметричность) - Если 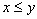и
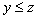, то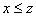 
(транзитивность)
Пример 3. Простым примером отношения порядка является отношение, задаваемое обычным неравенством 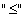на множестве вещественных чисел 
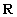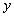. Заметим, что для любых чисел и выполняется либо 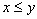, либо 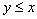, т.е. любые два числа сравнимы между собой. Такие отношения называются отношениями полного порядка.
Предикат данного отношения есть просто утверждение .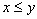
Пример 4. Рассмотрим на множестве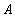 
всех сотрудников некоторого предприятия отношение, задаваемое следующим образом: сотрудник предшествует сотруднику 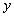тогда и только тогда, когда выполняется одно из условий:
|
|
|
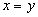
- является начальником (не обязательно непосредственным)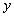
Назовем такое отношение "быть начальником". Легко проверить, что отношение "быть начальником" является отношением порядка. Заметим, что в отличие от предыдущего примера, существуют такие пары сотрудников и 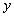, для которых не выполняется 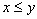ни , ни 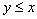(например, если и 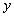являются сослуживцами). Такие отношения, в которых есть несравнимые между собой элементы, называют отношениями частичного порядка.
