Бинарные отношения (отношения степени 2)
Примеры отношений
В математике большую роль играют бинарные отношения, т. е. отношения, заданные на декартовом произведении двух множеств 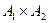 .
.
Определение 8. Отношение R на множестве A 2 называется отношением эквивалентности, если оно обладает следующими свойствами:
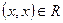 для всех
для всех 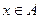 (рефлексивность);
(рефлексивность); - Если
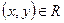 , то
, то 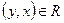 (симметричность);
(симметричность); - Если
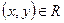 и
и 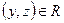 , то
, то 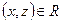 (транзитивность).
(транзитивность).
Обычно отношение эквивалентности обозначают знаком «=» или «≈» и говорят, что оно (отношение) задано на множестве A (а не на A 2). Условия 1 ÷ 3 в таких обозначениях выглядят более естественно:
 для всех
для всех 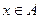 (рефлексивность);
(рефлексивность); - Если
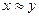 , то
, то 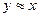 (симметричность);
(симметричность); - Если
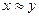 и
и 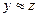 , то
, то 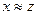 (транзитивность).
(транзитивность).
Легко доказывается, что если на множестве A задано отношение эквивалентности, то множество A разбивается на взаимно непересекающиеся подмножества, состоящие из эквивалентных друг другу элементов (классы эквивалентности).
Пример 1. Рассмотрим на множестве вещественных чисел 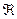 отношение, заданное просто равенством чисел. Предикат такого отношения:
отношение, заданное просто равенством чисел. Предикат такого отношения:
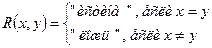 , или просто , или просто 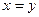 . .
|
Условия 1 ÷ 3, очевидно, выполняются, поэтому данное отношение является отношением эквивалентности. Каждый класс эквивалентности этого отношения состоит из одного числа.
Пример 2. Рассмотрим более сложное отношение эквивалентности. На множестве целых чисел Z зададим отношение «равенство по модулю n» следующим образом: два числа a и b равны по модулю n, если их остатки при делении на n равны. Например, по модулю 5 равны числа 2, 7, 12 и т. д.
Условия 1 ÷ 3 легко проверяются, поэтому равенство по модулю является отношением эквивалентности. Предикат этого отношения имеет вид:
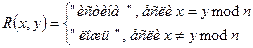 . .
|
Классы эквивалентности этого отношения состоят из чисел, дающих при делении на n одинаковые остатки. Таких классов ровно n:
| [0] = {0, n, 2n, …} |
| [1] = {1, n + 1, 2n + 1, …} |
| … |
| [n - 1] = {n - 1, n + n - 1, 2n + n - 1, …} |
 2014-02-02
2014-02-02 649
649








