Рис. 5.5.
Если реализация представляет собой совокупность дискретных значений стационарного случайного процесса, зафиксированных через равные промежутки времени 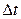 , то корреляционная функция определяется по формуле:
, то корреляционная функция определяется по формуле:
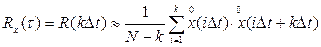 (5.12)
(5.12)
для получения достаточно достоверной информации о свойствах случайного процесса длину реализации 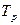 и интервал
и интервал 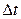 следует выбирать из условий;
следует выбирать из условий;
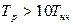 (5.13)
(5.13)
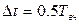 (5.14)
(5.14)
где 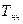 и
и 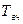 - периоды соответственно самой низкочастотной м высокочастотной составляющей сигнала.
- периоды соответственно самой низкочастотной м высокочастотной составляющей сигнала.
Функция 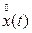 не является периодической, поэтому она не может быть разложена в ряд Фурье. С другой стороны, функция
не является периодической, поэтому она не может быть разложена в ряд Фурье. С другой стороны, функция 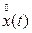 из-за неограниченной длительности не интегрируема и поэтому не может быть представлена интегралом Фурье. Для избежания этих трудностей вводится вспомогательная функция
из-за неограниченной длительности не интегрируема и поэтому не может быть представлена интегралом Фурье. Для избежания этих трудностей вводится вспомогательная функция 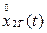 , которая совпадает с функцией
, которая совпадает с функцией 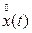 на интервале
на интервале 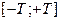 и равна нулю вне этого интервала:
и равна нулю вне этого интервала:
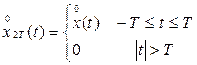 (5.15)
(5.15)
Функция 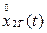 интегрируема и для нее существует прямое преобразование Фурье (интеграл Фурье):
интегрируема и для нее существует прямое преобразование Фурье (интеграл Фурье):
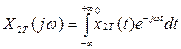 (5.16)
(5.16)
Спектральной плотностью мощности 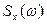 случайного сигнала (или просто спектральной плотностью) называется функция вида:
случайного сигнала (или просто спектральной плотностью) называется функция вида:
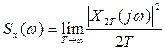 (5.17)
(5.17)
Спектральная плотность - это функция, характеризующая распределение средних значений квадратов амплитуд гармоник сигнала. Спектральная плотность обладает следующими свойствами:
1. Чем быстрее изменяется стационарный случайный процесс, тем шире график 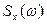 .
.
2. Отдельные пики на графике спектральной плотности свидетельствуют о наличии у случайного сигнала периодических составляющих.
3. Спектральная плотность является четной функцией:
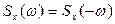 (5.18)
(5.18)
Спектральная плотность связана с дисперсией сигнала следующим соответствием:
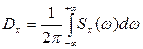 (5.19)
(5.19)
Экспериментально спектральная плотность определяется (вычисляется) по следующей схеме:
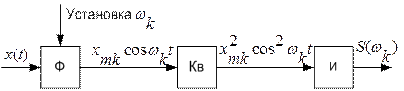
 2014-02-02
2014-02-02 989
989








