Корреляционная функция

Рис. 5.4.

Рис. 5.3.

Рис. 5.2.

Основные статистические характеристики стационарного случайного процесса

На рис. 5.2 представлена реализация стационарного случайного процесса.

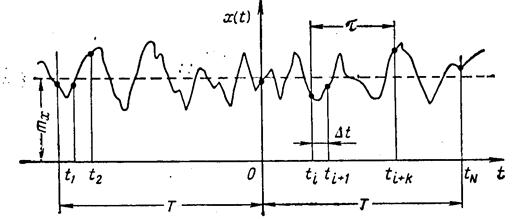
Определим основные статистические характеристики стационарного случайного процесса

Среднее значение сигнала на конечном интервале времени определяется как:

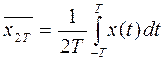(5.1)

Если интервал достаточно бодьшой, то среднее значение определяет математическое ожидание

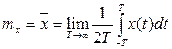(5.2)

Если на практике конечная реализация представлена в виде 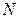дискретных значений, отделенных друг от друга равными промежутками времени 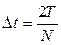, то среднее значение можно вычислить по формуле:

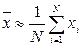(5.3)

Стационарный случайный процесс можно рассматривать как сумму постоянной составляющей и переменной составляющей , соответствующей отклонениям случайного сигнала от среднего:

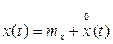(5.4)

Сигнал 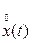называется центрированным случайным сигналом. Очевидно, сто среднее значение центрированного случайного сигнала равно нулю. Так как спектр реального сигнала 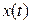совпадает со спектром центрированного случайного сигнала 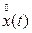, то во многих (но не во всех) задачах расчета автоматических систем можно вместо 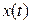рассматривать сигнал .

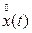Дисперсией 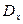называется среднее значение квадрата отклонений от математического ожидания :

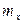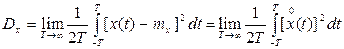(5.5)

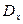- это мера разброса мгновенных значений сигнала около математического ожидания. Чем больше пульсация, тем больше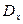

Средним квадратичным отклонением называется выражение вида:

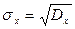(5.6)

Важным свойством статических характеристик является следующее:

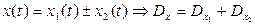(5.7)

Математическое ожидание 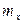и дисперсия 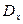являются важными характеристиками, но неисчерпывающими: по ним нельзя судить о скорости изменения сигнала во времени

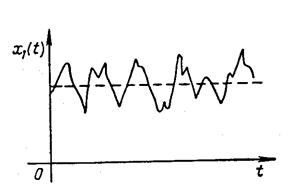
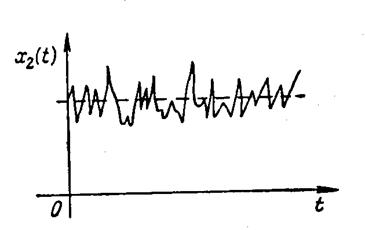
На рисунках 5.3, 5.4 представлены стационарные случайные процессы, имеющие равные математические ожидания и дисперсии (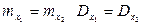). Однако из рисунков видно, что 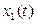изменяется медленнее, чем 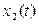. Интенсивность изменения стационарного случайного процесса во времени характеризуется следующими функциями: корреляционной функцией и функцией спектральной плотности.

Корреляционная (автокорреляционная) функция 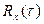- это математическое ожидание произведения мгновенных значений сигнала, разделенных промежутком времени :

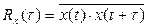(5.8)

Для центрированного сигнала 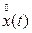корреляционная функция определяется по формуле:

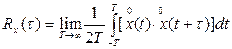(5.9)

где - варьируемый сдвиг по времени:

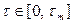(5.10)

Фиксированному соответствует определенное числовое значение .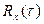

Корреляционная функция характеризует степень корреляции (связи) между предыдущими и последующими значениями сигнала.

Корреляционная функция обладает следующими свойствами:

1. При увеличении связь (корреляция) ослабевает.

2. Корреляционная функция убывает тем быстрее, чем быстрее изменяется случайный сигнал.

3. Корреляционная функция является четной функцией:

(5.11)

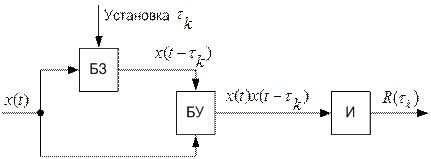
Экспериментально корреляционная функция определяют (вычисляют) по следующей схеме: