Классификация игр
Игры классифицируют по различным признакам в соответствии с конкретизацией видов и свойств составляющих характеристик игры.
Если в игре образование коалиций недопустимо или нецелесообразно, то такие игры называются бескоалиционными, однако бескоалиционными можно считать и игры, в которых совокупности коалиций действия и коалиций интересов совпадают. В этом случае каждую коалицию можно считать игроком (поскольку это есть заинтересованная сторона).
Таким образом, бескоалиционная игра, которую называют также просто игрой, представляет собой (как отмечалось в предыдущем параграфе) совокупность множества игроков, множеств их стратегий и наборов их функций выигрыша.
В бескоалиционных играх цель каждого игрока - получение максимально возможного индивидуального выигрыша. Даже если игроки и объединяются в коалиции, то такие коалиции преследуют только интересы отдельных игроков, вошедших в коалицию, и основная задача бескоалиционной игры состоит в дележе общего выигрыша между игроками.
В играх, по существу коалиционных, совокупности коалиций действия и коалиций интересов различны. В коалиционных играх игроки стремятся максимизировать выигрыши коалиций без последующего их распределения между игроками.
В дальнейшем мы будем рассматривать только бескоалиционные игры.
Как уже отмечалось в предыдущем параграфе, игры можно классифицировать по числу игроков: парные игры, в которых два игрока, и множественные игры, в которых число игроков больше двух. Если в парной игре игроки преследуют противоположные цели, то игра называется антагонистической. В такой игре один из игроков выигрывает ровно столько, сколько проигрывает другой. Поэтому, функции выигрышей 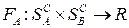 и
и  соответственно игроков А и В связаны между собой соотношением
соответственно игроков А и В связаны между собой соотношением
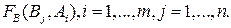 (3.1)
(3.1)
Из равенства (3.1) следует, что ,и потому антагонистические игры называют также играми двух сторон с нулевой суммой выигрыша.
,и потому антагонистические игры называют также играми двух сторон с нулевой суммой выигрыша.
В силу равенства (3.1) функция выигрыша игрока В полностью определяется функцией выигрыша игрока А и, следовательно, антагонистическая игра с игроками А и В вполне определяется совокупностью 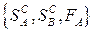 , состоящей из множества
, состоящей из множества 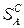 стратегий игрока А, множества
стратегий игрока А, множества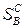 стратегий игрока В и функции
стратегий игрока В и функции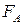 выигрыша игрока А.
выигрыша игрока А.
Антагонистические игры с точки зрения математического моделирования являются достаточно простыми и потому наиболее хорошо изученными.
Можно разделить игры на классы по мощности множеств стратегий игроков. Как уже отмечалось, если множество стратегий каждого игрока конечно, то игра называется конечной. В противном случае она называется бесконечной.
В конечной антагонистической игре с игроками А и В можно строки некоторой матрицы (таблицы) поставить в соответствие стратегиям А, игрока А, а столбцы - в соответствие стратегиям 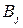 игрока В. Если на пересечениях строк и столбцов расставить значения
игрока В. Если на пересечениях строк и столбцов расставить значения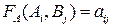 функции выигрыша
функции выигрыша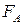 игрока А, соответствующие ситуациям
игрока А, соответствующие ситуациям 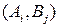 , то получим матрицу А, которая называется матрицей выигрышей игрока А.
, то получим матрицу А, которая называется матрицей выигрышей игрока А.
Аналогичным образом, из значений функции выигрыша
функции выигрыша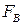 игрока В, можно составить матриц В выигрышей игрока В.
игрока В, можно составить матриц В выигрышей игрока В.
В силу равенства (3.1) 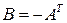 (т. е. матрица В противоположна транспонированной матрице А). Таким образом, матрица В определяется матрицей А и потому конечная антагонистическая игра характеризуется фактически только одной матрицей выигрышей и в силу этого называется матричной.
(т. е. матрица В противоположна транспонированной матрице А). Таким образом, матрица В определяется матрицей А и потому конечная антагонистическая игра характеризуется фактически только одной матрицей выигрышей и в силу этого называется матричной.
Итак, матричная игра полностью определяется совокупностью 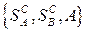 , состоящей из множества
, состоящей из множества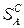 стратегий игрока А, множества
стратегий игрока А, множества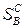 стратегий игрока В и матрицы А выигрышей игрока А.
стратегий игрока В и матрицы А выигрышей игрока А.
Если в конечной бескоалиционной игре участвуют два игрока А и В с различными, но не противоположными интересами, то матрицы их выигрышей А и В уже не будут удовлетворять равенству 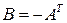 и потому такую игру называют биматричной. Таким образом, биматричная игра вполне задается совокупностью
и потому такую игру называют биматричной. Таким образом, биматричная игра вполне задается совокупностью 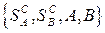 , состоящей из множества стратегий игрока А, множества
, состоящей из множества стратегий игрока А, множества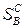 стратегий игрока В и уже двух матриц А и В выигрышей игроков А и В.
стратегий игрока В и уже двух матриц А и В выигрышей игроков А и В.
Рассмотрим парную игру с игроками А и В. Пусть игрок А имеет т стратегий -  , а (противник) игрок В - п стратегий
, а (противник) игрок В - п стратегий 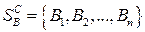 . Натуральные числа т и п в общем случае никак не связаны между собой.
. Натуральные числа т и п в общем случае никак не связаны между собой.
Если каждый из игроков А и В сознательно определенным образом выбирает стратегии 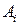 и
и 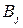 соответственно, то сложившаяся ситуация (в чистых стратегиях)
соответственно, то сложившаяся ситуация (в чистых стратегиях) 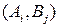 однозначно определяет выигрыш игрока А, выражающийся действительным числом
однозначно определяет выигрыш игрока А, выражающийся действительным числом 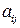 , которое одновременно является и проигрышем игрока В. А число
, которое одновременно является и проигрышем игрока В. А число 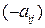 выражает проигрыш игрока А и выигрыш игрока В. Если число
выражает проигрыш игрока А и выигрыш игрока В. Если число 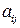 отрицательно, то в принятой нами формализованной терминологии оно будет представлять отрицательный выигрыш игрока А, а по сути - его проигрыш. Числа
отрицательно, то в принятой нами формализованной терминологии оно будет представлять отрицательный выигрыш игрока А, а по сути - его проигрыш. Числа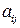 - это значения функции выигрыша
- это значения функции выигрыша 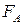 игрока А:
игрока А: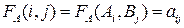 . Ходы игроков с сознательным выбором одной из возможных своих чистых стратегий называют иногда личными ходами.
. Ходы игроков с сознательным выбором одной из возможных своих чистых стратегий называют иногда личными ходами.
Выигрыши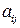 ,
, 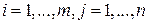 , можно расположить в виде матрицы, номера строк которой соответствуют номерам стратегий игрока А, а номера столбцов - номерам стратегий игрока В.
, можно расположить в виде матрицы, номера строк которой соответствуют номерам стратегий игрока А, а номера столбцов - номерам стратегий игрока В.
| А = |   Ai Ai | 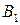 | 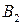 | … | 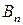 | (4.1) |
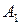 | 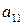 | 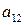 | … | 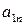 | ||
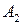 | 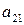 | 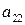 | … |  | ||
| … | … | … | … | … | ||
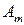 |  | 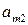 | ... | 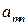 |
Матрица А называется матрицей выигрышей игрока А. Обозначим через 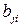 значения функции выигрыша Рв игрока В, т. е. ед, 0 = Рв (В;, Ад = =1,..., п, 1 =1,..., т. Тогда матрица выигрышей игрока В будет иметь вид
значения функции выигрыша Рв игрока В, т. е. ед, 0 = Рв (В;, Ад = =1,..., п, 1 =1,..., т. Тогда матрица выигрышей игрока В будет иметь вид
| B = | Ai   | 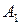 | 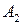 | … | 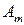 |
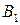 |  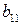 | 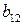 | … | 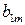 | |
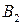 |  | 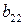 | … |  | |
| … | … | … | … | … | |
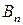 | 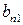 | 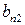 | ... | 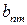 |
Если рассматриваемая игра – антагонистическая (т.е. с нулевой сумой выигрышей), то функции выигрышей 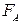 и
и  игроков A и B связаны между собой равенством (3.1) и, следовательно,
игроков A и B связаны между собой равенством (3.1) и, следовательно,
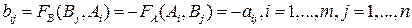
Эти равенства означают, что матрица выигрышей B игрока B является противоположной транспонированной матрице A:
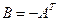 .
.
Таким образом, матрица В вполне определяется матрицей А. Матрицу А также называю матрицей игры, или платежной матрицей. Матрица А имеет размер 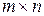 , где первая компонента размера
, где первая компонента размера 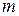 указывает на число строк (т.е. число стратегий игрока А), а вторая
указывает на число строк (т.е. число стратегий игрока А), а вторая  - на число столбцов (число стратегий игрока В). Поэтому часто такую игру называют
- на число столбцов (число стратегий игрока В). Поэтому часто такую игру называют 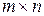 - игрой.
- игрой.
Отметим, что матрица игры существенно зависит от упорядочения множеств 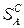 и
и 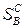 стратегий игроков А и В. При другой нумерации стратегий этих множеств мы получим, вообще говоря, другую матрицу игры. Так что одна и та же игра может описываться различными матрицами. Но при всех возможных матрицах игры функция
стратегий игроков А и В. При другой нумерации стратегий этих множеств мы получим, вообще говоря, другую матрицу игры. Так что одна и та же игра может описываться различными матрицами. Но при всех возможных матрицах игры функция 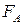 выигрыша игрока А остается одной и той же, определенной на декартовом произведении
выигрыша игрока А остается одной и той же, определенной на декартовом произведении 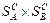 с множеством значений в множестве действительных чисел R. Это замечание относится и к функции
с множеством значений в множестве действительных чисел R. Это замечание относится и к функции 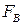 выигрыша игрока В.
выигрыша игрока В.
Построение матрицы выигрышей может представлять весьма нетривиальную задачу, особенно для игр большой размерности. В принципе же всякую конечную антагонистическую игру можно привести к матричной форме.
Матрица игры А формируется в зависимости от значений функции выигрыша 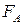 , которая может задаваться таблично, аналитически (в виде формулы) или словестно-описательным способом.
, которая может задаваться таблично, аналитически (в виде формулы) или словестно-описательным способом.
Для того чтобы совокупность 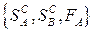 , представляющая антагонистическую игру, стала обозримой, необходимо перечислить возможные стратегии игроков, т.е. сформировать множества
, представляющая антагонистическую игру, стала обозримой, необходимо перечислить возможные стратегии игроков, т.е. сформировать множества 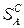 и
и 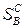 , и формализовать правила, по которым развивается конфликт, в виде функции выигрыша
, и формализовать правила, по которым развивается конфликт, в виде функции выигрыша 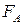 .
.
Пример 4.1 (антагонистическая конкуренция) [7]. Фирма А производит некоторый сезонный товар, имеющий спрос в течение  единицвремени, и который она может поставить на рынок в один из моментов
единицвремени, и который она может поставить на рынок в один из моментов 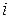
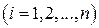 (см. рис. 4.1).
(см. рис. 4.1).
Для конкурентной борьбы с фирмой А дочерняя фирма В концерна D не заботясь о собственных доходах, производит аналогичный товар, который поступает на рынок в один из моментов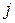
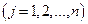 . Цель фирмы В - разорение фирмы А, после чего, используя капитал концерна D она может легко наверстать упущенное. Единственным законным средством фирмы В в конкурентной борьбе является выбор момента поставки товара на рынок, так как понижение цены на поставляемый товар запрещено определенным соглашением. Для разорения фирмы А фирма В должна минимизировать ее дохода. Пусть технология выпуска товара такова, что чем дольше он находится в производстве, и, следовательно, позже поступает на рынок, тем выше его качество, а реализуется товар только более высокого качества (так как цена на товары разного качества одна и та же). Доход от продажи товара в единицу времени составляет с денежных единиц.
. Цель фирмы В - разорение фирмы А, после чего, используя капитал концерна D она может легко наверстать упущенное. Единственным законным средством фирмы В в конкурентной борьбе является выбор момента поставки товара на рынок, так как понижение цены на поставляемый товар запрещено определенным соглашением. Для разорения фирмы А фирма В должна минимизировать ее дохода. Пусть технология выпуска товара такова, что чем дольше он находится в производстве, и, следовательно, позже поступает на рынок, тем выше его качество, а реализуется товар только более высокого качества (так как цена на товары разного качества одна и та же). Доход от продажи товара в единицу времени составляет с денежных единиц.
Требуется построить функцию выигрыша фирмы А, где под выигрышем понимается в данном случае доход этой фирмы, зависящий от складывающихся ситуаций. Используя функцию выигрыша, надо составить матрицу игры для случая 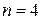 и выписать конкретный вид этой матрицы, который она приобретает в случае, когда доход
и выписать конкретный вид этой матрицы, который она приобретает в случае, когда доход 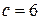 денежным единицам.
денежным единицам.
Пример 4.2. На каждой из двух торговых баз ассортиментный минимум составляет один и тот же набор из  видов товаров. Каждая база должна поставить в свой магазин только один из этих видов товара. Магазины, обозначим их А и В, конкурируют между собой. Один и тот же вид товара в обоих магазинах продается по одной и той же цене. Однако, товар, поставляемый в магазин В, более высокого качества. Если магазин А завезет с базы товар
видов товаров. Каждая база должна поставить в свой магазин только один из этих видов товара. Магазины, обозначим их А и В, конкурируют между собой. Один и тот же вид товара в обоих магазинах продается по одной и той же цене. Однако, товар, поставляемый в магазин В, более высокого качества. Если магазин А завезет с базы товар 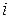 -го вида
-го вида 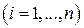 , отличный от товара
, отличный от товара 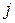 -го вида
-го вида  , завезенного в магазин В, то товар го вида будет пользоваться спросом и магазин А от его реализации получит прибыль
, завезенного в магазин В, то товар го вида будет пользоваться спросом и магазин А от его реализации получит прибыль 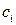 денежных единиц. Если же в магазины А и В завезены товары одинакового вида
денежных единиц. Если же в магазины А и В завезены товары одинакового вида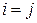 , то товар
, то товар 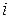 -го вида в магазине А спросом пользоваться не будет, поскольку такой же товар, по такой же цене, но более высокого качества, можно купить в магазине В, и потому магазин А понесет убытки по транспортировке, хранению и возможно порче товара
-го вида в магазине А спросом пользоваться не будет, поскольку такой же товар, по такой же цене, но более высокого качества, можно купить в магазине В, и потому магазин А понесет убытки по транспортировке, хранению и возможно порче товара 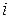 -го вида в размере
-го вида в размере 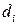 денежных единиц.
денежных единиц.
Требуется формализовать данную конфликтную ситуацию и построить матрицу игры при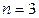 .
.
 2014-02-02
2014-02-02 1120
1120








