2014-02-02
932
Пусть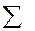 
есть алгебра событий, определенная в пункте 1.
Определение. Вероятностью называется функция (на 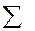), которая каждому случайному событию 
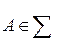ставит в соответствие число 
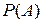и удовлетворяет следующим аксиомам:
Аксиома 1.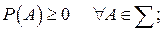 
Аксиома 2.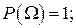 
Аксиома 3. Если случайные события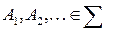 
попарно несовместимы (то есть 
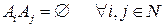т. ч. 
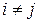) то
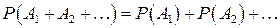
Замечание. Если имеется бесконечное число попарно несовместных событий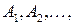 
то в правой части последнего ряда стоит сумма ряда.
Аксиомы 1-3 вместе с понятием алгебры событий 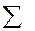являются фундаментом всей теории вероятности. Все утверждения и теоремы выводятся из них логическим путем.
Приведем некоторые из этих утверждений и теорем.
Утверждение 1.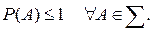 
Доказательство.
Так как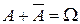 
и события 
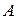и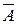 
несовместимы, то из аксиом 1, 2, 3 следует
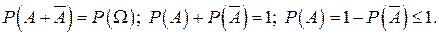
Утверждение доказано.
Замечание. При доказательстве утверждения 1 выведена полезная формула
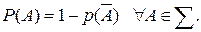
Утверждение 2. (Вероятность суммы событий).
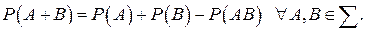
Доказательство.
Заметим сначала, что множества 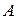и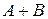 
можно представить в виде суммы непересекающихся множеств:
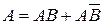и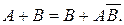 
Далее из аксиомы сложения следует, что
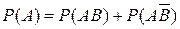и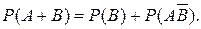 
Если из второго равенства вычесть первое, то получим требуемое равенство. Утверждение доказано.
Тема 2: Условная вероятность. Независимые события. Формула полной вероятности и Байеса.
