Зависимые и независимые события

Классическое определение вероятности.

Вероятность события –это количественная мера, которая вводится для сравнения событий по степени возможности их появления.

Событие, представимое в виде совокупности (суммы) нескольких элементарных событий, называется составным.

Событие, которое нельзя разбить на более простые, называется элементарным.

Событие называется невозможным, если оно не происходит никогда в условиях данного эксперимента (испытания).

Достоверные и невозможные события не являются случайными.

Совместные события – несколько событий называют совместными, если в результате эксперимента наступление одного из них не исключает появления других.

Несовместные события – несколько событий называют несовместными в данном эксперименте, если появление одного из них исключает появление других. Два события называются противоположными, если одно из них происходит тогда и только тогда, когда не происходит другое.

Вероятностью события А – Р(А) – называется отношение числа m элементарных событий (исходов), благоприятствующих появлению события А, к числу n всех элементарных событий в условиях данного вероятностного эксперимента.

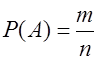(1)

Из определения вытекают следующие свойства вероятности:

1. Вероятность случайного события есть положительное число, заключенное между 0 и 1:

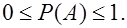(2)

2. Вероятность достоверного события 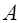равна 1: 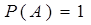(3)

3. Если событие невозможное, то его вероятность равна

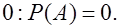(4)

4. Если события 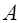и 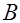несовместны, то

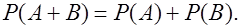(5)

5. Если события А и В совместны, то вероятность их суммы равна сумме вероятностей этих событий без вероятности их совместного наступления:

Р(А+В) = Р(А) +Р(В) - Р(АВ) (6)

6. Есл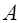и и 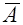- противоположные события, то 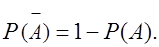(7)

7. Сумма вероятностей событий А₁, А₂, …, А_{n ,} образующих полную группу, равна 1:

Р(А₁) + Р(А₂) + …+ Р(А_n) = 1. (8)

В экономических исследованиях значения 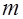и 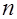в формуле могут интерпретироваться по-другому. При статистическом определении вероятности события 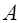под 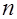понимается количество наблюдений результатов эксперимента, в которых событие 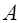встречалось ровно 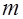раз. В этом случае отношение 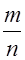называется относительной частотой (частостью) события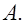

События А, В называются независимыми, если вероятности каждого из них не зависит от того, произошло или нет другое событие. Вероятности независимых событий называются безусловными.

События А, В называются зависимыми, если вероятность каждого из них зависит от того, произошло или нет другое событие. Вероятность события В, вычисленная в предположении, что другое событие А уже осуществилось, называется условной вероятностью.

Если два события А и В – независимые, то справедливы равенства:

Р(В) = Р(В/А), Р(А) = Р(А/В) или Р(В/А) – Р(В) = 0 (9)

Вероятность произведения двух зависимых событий А, В равна произведению вероятности одного из них на условную вероятность другого:

Р(АВ) = Р(В)? Р(А/В) или Р(АВ) = Р(А)? Р(В/А) (10)

Вероятность события В при условии появления события А:

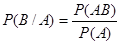(11)

Вероятность произведения двух независимых событий А, В равна произведению их вероятностей:

Р(АВ) = Р(А)? Р(В) (12)

Если несколько событий попарно независимы, то отсюда еще не следует их независимость в совокупности.

События А₁, А₂, …, А_n (n>2) называются независимыми в совокупности, если вероятность каждого из них не зависит от того, произошли или нет любые события из числа остальных.

Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:

Р(А₁?А₂?А₃?…?А_n) = Р(А₁)?Р(А₂)?Р(А₃)?…?Р(А_n). (13)