2014-02-02
1733
В предыдущем параграфе мы рассмотрели классическое определение вероятности для случая, когда пространство элементарных событий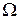 
конечно. Однако во многих практических ситуациях пространство 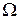является бесконечным (даже несчетным).
Например, пусть опыт состоит в произведении выстрела по круглой мишени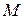 
. В этом случае пространство элементарных событий 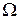бесконечно. Оно совпадает с множеством точек .
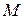Определение вероятности событий в общем случае (для произвольных пространств 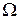) строится аксиоматическим методом.
Система аксиом теории вероятности была построена в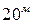 
веке выдающимся советским математиком, академиком А. Н. Колмогоровым.
В аксиоматике А. Н. Колмогорова случайное событие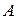 
отождествляется с соответствующим подмножеством пространства элементарных событий. Например, случайное событие, состоящее в том, что «на игральном кубике выпало нечетное число очков» есть подмножество 
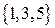пространства элементарных событий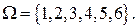 
Такой подход удобен тем, что благодаря ему операциям над случайными событиями, таким как, сумма и произведение, соответствуют операции объединения (или суммы) и пересечения (произведения) множеств.
Пусть задано некоторое множество 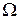. Его будем называть пространством элементарных событий, а элементы 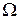будем называть элементарными событиями.
Для любого подмножества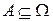 
будем обозначать через 
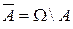- дополнение множества .
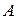Случайными событиями будем называть систему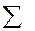 
подмножеств множества 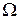, такую что
1. 
;
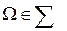2. Если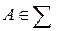 
, то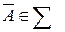 
;
3. Если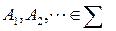 
, то 
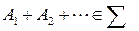и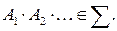 
Напомним, что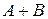 
и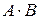 
также обозначаются, как 
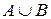и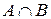 
соответственно.
Замечание. Если 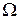конечно, то система 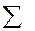представляет собой все возможные подмножества .
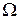Определим в общем случае понятия совместных, несовместных, достоверных и недостоверных событий.
Определение. Рассмотрим случайные события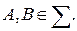 
Они называются несовместными, если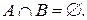 
Определение. Пусть 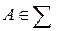. Тогда события 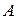и 
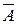называют противоположными. Событие 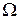называется достоверным, а событие 
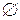(пустое множество) называется невозможным.
Определение. Система подмножеств 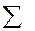со свойствами 1, 2, 3 называется алгеброй событий.
