Равномерное распределение на отрезке

Примеры непрерывных случайных величин.

Определение. Случайная величина X называется равномерно распределенной на отрезке 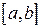, если она имеет плотность вероятности следующего вида:

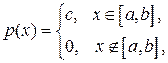
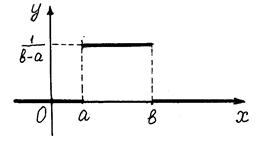
где 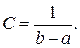График 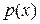изображен на рисунке.

Пусть отрезок 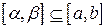и длина его равн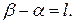а Тогда

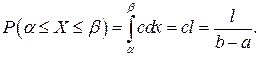
Таким образом, вероятность попаданий значений X в любую часть отрезка 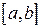пропорционально длине этой части.

Приведем пример равномерно распределенной случайной величины.

Пусть 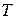есть интервал движения между троллейбусами на городской линии. Пусть случайная величина X равна времени ожидания троллейбуса на остановке. Случайная величина X равномерно распределена на отрезке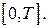

Нормально распределенная величина.

На практике широко распространены случайные величины, плотность распределения вероятности которых определяется функцией

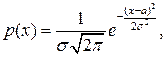
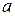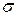где и - некоторые постоянные числа и 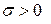. В этом случае говорят, что случайная величина X распределена по закону Гаусса или по нормальному закону.

Утверждение. Плотность вероятности нормально распределенной случайной величины удовлетворяет свойству .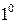

Доказательство.

.

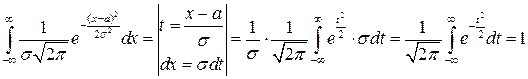(см. замечание на стр. 18). Утверждение доказано.

Если X есть нормально распределенная величина с параметрам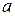и и 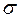, то говорят, что X распределена по закону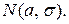

График плотности вероятности нормального распределения называют нормальной кривой.

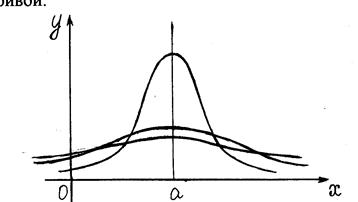
Он симметричен относительно прямо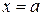й и при 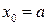достигает максимума. При увеличении 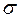кривая становится более пологой. На рисунке представлены нормальные кривые при При любом 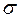площадь под кривой, согласно свойства 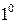, равна 1.

Задача. Доказать, что точки 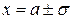являются точками перегиба.

Утверждение. Если X распределена по закону 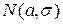, то

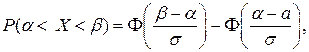(10)

где 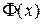есть функция Лапласа, определенная на стр. 62.

Доказательство.

=

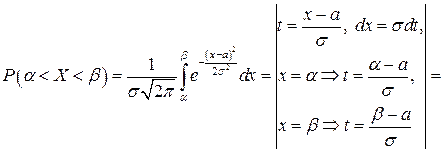
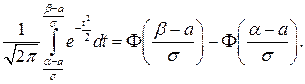
Утверждение доказано.

Следствие. Если X распределена по закону 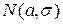, то

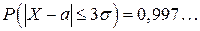(11)

Доказательство.

Согласно (10)

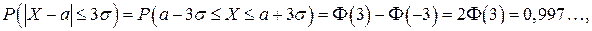
где 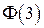найдено по таблице.

Утверждение доказано.

Таким образом, событие, состоящее в том, что 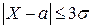является практически достоверным. Это правило называется «правилом трех сигм».

Нормально распределенные случайные величины играют важную роль в теории вероятностей. Дело в том, что распределение многих случайных величин, встречающихся в жизни, близко к нормальному распределению. Этот факт является следствием Центральной предельной теоремы теории вероятностей, которую доказал в 1901 году выдающийся русский математик А.М. Ляпунов. В общих чертах содержание формулировки Центральной предельной теоремы может быть высказано следующим образом.

Распределение суммы большого числа независимых случайных величин (не обязательно нормально распределенных) при весьма общих условиях близко к нормальному распределению.

Этим и определяется особая роль, нормально распределенных случайных величин, поскольку с суммами большого числа случайных слагаемых приходится часто иметь дело и в самой теории вероятностей и в ее приложениях.

Проиллюстрируем вышесказанное на следующем примере. Рассмотрим производство, на котором изготовляются большие партии однотипных изделий. Все наиболее существенные характеристики выпускаемых изделий должны соответствовать определенному стандарту. Однако в действительности наблюдаются отклонение от стандарта, которые порождаются причинами случайного характера (следует учесть, что выпуск изделий связан, как правило, со многими операциями, некоторые из которых не могут быть выполнены абсолютно точно). Каждая из этих причин сама по себе порождает ничтожную ошибку X, но, складываясь, такие ошибки, могут давать ощутимые отклонения от стандарта. Здесь, опираясь наЦентральную предельную теорему, можно утверждать, что суммарное отклонение от стандарта представляет случайную величину, закон распределения которой близок к нормальному закону распределения.

Можно привести много подобных примеров из жизни. Они объясняют, почему нормальный закон так часто встречается в практических задачах.

Тема 5: Числовые характеристики случайных дискретных величин: математическое ожидание, дисперсия,