Определение. Случайная величина X называется непрерывной, если ее функция распределения 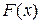 непрерывна при всех
непрерывна при всех 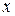 .
.
Утверждение. Если X непрерывная случайная величина, то 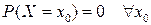 , то есть вероятность каждого отдельного значения непрерывной случайной величины равна 0.
, то есть вероятность каждого отдельного значения непрерывной случайной величины равна 0.
Доказательство.
Легко видеть, что
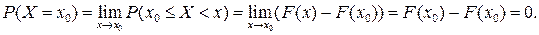
Утверждение доказано.
Определение. Пусть функция 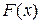 дифференцируемая на всей
дифференцируемая на всей 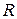 , за исключением, быть может, конечного или счетного множества точек
, за исключением, быть может, конечного или счетного множества точек 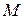 . Плотностью вероятности случайной величины X называется функция
. Плотностью вероятности случайной величины X называется функция
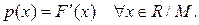
Для большинства непрерывных случайных величин имеет место формула
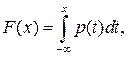 (9)
(9)
где справа в формуле стоит несобственный интеграл.
Задача. Доказать формулу (9) в случае, когда 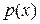 непрерывна на
непрерывна на 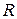 .
.
Из свойств  функции распределения вытекают следующие свойства плотности вероятности.
функции распределения вытекают следующие свойства плотности вероятности.
Если 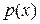 есть плотность вероятности непрерывной случайной величины X, то
есть плотность вероятности непрерывной случайной величины X, то
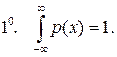
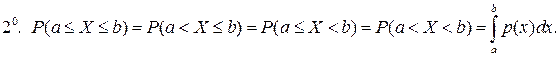
 2014-02-02
2014-02-02 360
360








