Динамическое программирование

1.1 Теоретические сведения. Программа “BELLMAN”

Динамическое программирование – это метод поиска опти­мальных решений для широкого круга задач, возникающих в раз­личных областях практической деятельности [1,2,3]. Для его успешного применения необходимо построить математическую модель за­дачи и убедиться в соблюдении условий применимости этого ме­тода, так как он не универсален.

Для освоения метода, иллюстрации его возможностей и ус­ловий применимости разработана специальная обучающая ком­пьютерная программа “BELLMAN”.

Цель разработчиков программы и настоящих методических указаний состоит в том, чтобы помочь пользователю программы в освоении идеи метода и конкретного алгоритма динамического программирования.

Обучение ведётся на конкретной задаче поиска оптимального пути на двумерной сетке, которую можно рассматривать как модель многих практических задач оптимизации.

Программа позволяет выполнить расчёт и найти оптимальный путь при различных размерах сетки. Для иллюстрации эффективности метода динамического программирования в программе реализован также и метод полного перебора вариантов.

Для наглядности реализация алгоритмов полного перебора и динамического программирования сопровождается графическим изображением процесса поиска оптимального варианта.

Компьютерная программа даёт возможность не только понять принцип оптимальности Р.Беллмана, уяснить преимущества метода динамического программирования по сравнению с полным перебором вариантов, но и проверить свои знания в данной области.

Программа не предъявляет высоких требований к объёму оперативной памяти компьютера и его быстродействию и может использоваться практически на любой персональной ЭВМ.

Программа предназначена для самостоятельного изучения студентами динамического программирования и должна рассматриваться как вспомогательное средство для выполнения курсовой работы и закрепления знаний, полученных в процессе освоения лекционного материала и/или чтения соответствующей литературы.

В принципе никаких специальных знаний, выходящих за пределы программы средней школы, не требуется. Можно начать знакомство с динамическим программированием непосредственно с обучающей программы с последующим изучением других источников, но целесообразно предварительно проработать лекционный материал и/или прочесть соответствующую литературу.

Вопросы, которые программа задаёт пользователю, относятся к пониманию сущности принципа оптимальности и области применения динамического программирования. Ответы непосредственно на эти конкретные вопросы вряд ли можно найти в литературных источниках, но получив с помощью программы информацию о своих ошибках и в конечном итоге правильный ответ, пользователь всегда сможет вникнуть в существо дела.

Программа может быть полезна также преподавателю, как для иллюстрации возможностей динамического программирования, так и для проверки понимания студентами особенностей метода, условий его применимости и характеристики области использования. Она даёт пользователю возможность реально представить сложность решения практических задач большой размерности, в конкретных расчётах ощутить “проклятие размерности”.

Программа предлагает несколько тестов, фиксирует правильные и неправильные ответы, даёт возможность проверить знания динамического программирования, поразмыслить над ошибками и закрепить полученные знания.

Вместе с тем программа и настоящие методические указания по её использованию не могут заменить изучение лекционного ма-териала и литературных источников.

Программа предлагает пользователю простую задачу поиска оптимального пути на двумерной прямоугольной сетке, в которой разрешены переходы из одного узла в другой только по горизонтали (вправо) или по вертикали (вверх)[3].

Заданы затраты на каждый из возможных переходов и требуется найти путь c минимальными суммарными затратами из ле-вого нижнего угла сетки (рис. 1 точка А) в правый верхний угол (точка В). Такой путь называется оптимальным.

Узлы сетки пронумерованы так, как показано на рис.1, где m и n задают соответственно вертикальный и горизонтальный размеры сетки.

Затраты на переход в узел i, j по горизонтали (из узла i, j-1) cоставляют g_ij, а по вертикали (из узла i-1,j) -v_ij. В точке А соответствующие величины равны нулю. Таким образом, исходные данные в этой задаче: m,n плюс все шаговые затраты g_ij и

v_ij (i = 0,1,2,…, m; j = 0,1,2, …, n). Всего n(m+1) чисел g_ij и m(n+1) чисел v_ij, то есть всего 2mn+m+n переходов и соответст-вующих им затрат.

(m,0) В (m,n)

(i,0) g_ij(i,j)

v_ij

(2,0)

(1,0) (1,n)

A(0,0) (0,j) (0,n)

Рис. 1. Задача поиска оптимального пути.

Вначале обсуждается возможность решения этой задачи ме-тодом полного перебора вариантов возможных путей из точки А в точку В и устанавливается бесперспективность этого метода уже при величинах m и n порядка 10.

Следующая идея состоит в том, чтобы из точки А идти в том направлении, которое требует минимальных затрат на первом шаге, не думая о затратах на последующих шагах, и так в каждой точке. То есть рассматривать только затраты на данном шаге и выбирать тот переход, для которого на данном шаге затраты минимальны. Пользователь должен убедиться в ошибочности этой идеи даже при m=n=1.

Далее программа формулирует принцип оптимальности Р. Беллмана и соответствующий алгоритм решения поставленной задачи, а также позволяет пользователю прямым расчётом практически убедиться в преимуществах метода динамического программирования по сравнению с методом полного перебора варантов.

Принцип оптимальности Р. Беллмана сформулирован для широкого круга задач управления, распределения ресурсов, проектирования и др. и вообще задач принятия решений в многошаговых (многоэтапных) процессах. Если задано начальное (точка А) и конечное (точка В) состояния некоторой системы и переход из начального в конечное состояние осуществляется в несколько промежуточных этапов, на каждом из которых система может находиться в одном из различных состояний, и каждому переходу на каждом этапе можно сопоставить некоторые затраты, то задача состоит в том, чтобы выбрать такой путь (то есть все промежу-точные состояния), при котором некоторая количественная оце-нка этого пути достигает минимума.

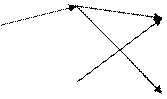
Предположим, для начала, что количественная оценка пути это суммарные затраты (сумма затрат по этапам, т.е. сумма шаговых затрат). Пусть на первом этапе из начального состояния (точка А) можно перейти в некоторое конечное число состояний (четыре точки на вертикали 1 рис. 2) с соответствующими затратами. Далее аналогично из состояний первого этапа (результатов первого шага) можно перейти в конечное число состояний (три точки на вертикали 2) и т.д., вплоть до конечного этапа, на котором из всех возможных состояний возможен переход только в конечное состояние (точка В).

В конкретной задаче может быть так, что для каждого или некоторых промежуточных состояний (например, точка С) дальнейшие переходы зависят от того каким образом система была переведена в это состояние (например, переход СД возможен, если пришли в точку С из точки M, и невозможен, если пришли в точку С из точки N). Но может быть и так, что для всех промежуточных состояний дальнейшие переходы никак не зависят от того как система попала в это состояние.

M

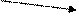
А C

В

N D

1 2 3 k-1

Рис. 2. Иллюстрация метода динамического программирования

В первом случае говорят о “задачах с предысторией”, а во втором случае об отсутствии предыстории, точнее о том, что предыстория не имеет значения для дальнейшего поведения системы. Принцип Р.Беллмана гласит “если в каждом из состояний дальнейшее поведение системы не зависит от того, как она попала в это состояние, то дальнейшая траектория должна быть оптимальной”. Это означает, что речь идёт только о системах “без предыстории”. В этом случае из каждого промежуточного состояния можно отдельно, независимо от пройденных этапов, решать задачу поиска оптимального пути в конечное состояние.

В рассматриваемой задаче поиска оптимального пути на сетке предыстория не имеет значения, так как из каждого узла, независимо от того, как мы попали в этот узел, можно перейти в соседний с известными заранее дополнительными затратами. Поэтому в каждом из промежуточных узлов из вариантов, сходя-щихся в этом узле, можно выбрать лучший (с минимальными затратами на путь от точки А до данного узла), худший вариант отбросить и все его продолжения не рассматривать.

Если при сравнении вариантов они окажутся равноценны по затратам, то можно оставить любой из них[1,2].

В каждом промежуточном узле, достигаемом на очередном шаге, запоминаем суммарные затраты на путь из точки А по лучшему варианту и направление откуда пришли (0- пришли по горизонтали, 1- пришли по вертикали). На последнем (m + n) шаге попадаем в точку В, в которой сходятся два варианта (пришли слева или снизу). Из них выбираем вариант с наименьшими затратами. Это и есть затраты, соответствующие оптимальному пути. Сам путь восстанавливается обратным разворотом следующим образом.

В точке В знаем направление (откуда пришли по оптимальному варианту). Если по горизонтали (запомнили 0), то смещаемся из точки В влево (по горизонтали), а если по вертикали, т.е. (запомнили 1), то смещаемся вниз (по вертикали). В любом случае в той точке, где мы окажемся, тоже есть направление (запомнили 0 или 1), что позволяет сделать ещё шаг в обратном направлении по оптимальному пути и в конечном итоге восстановить весь оптимальный путь.

Вспомним, что в качестве количественной оценки пути из точки А в точку В мы взяли сумму шаговых затрат. Очевидно, что если вместо суммы будет её монотонно возрастающая функция, то в алгоритме принципиально ничего не изменится, так как задачу можно решать по- прежнему и только после того как, она будет решена, вычислить значение заданной монотонно возрастающей функции от найденной минимальной суммы затрат по оптимальному пути.

Возможны, однако, задачи, в которых количественную оценку пути можно найти только зная весь путь полностью и не удаётся свести вычисление этой оценки к оценкам на отдельных шагах.