Теорема Котельникова

Любую функцию f(t), состоящую из частот от 0 до f_c (т. е. с ограниченным спектром), можно передавать с любой точностью (в зависимости от типа ФНЧ) с помощью чисел, следующих друг за другом через интервал 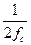, если f_д не менее чем в 2 раза превосходит f_c спектра. Т. е. сигнал с ограниченным спектром может быть восстановлен по его дискретным отсчетам, если частота этих отсчетов будет выбрана не меньше, чем удвоенное значение частоты спектра сигнала ().

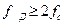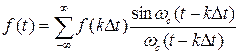, здесь 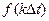– выборки, 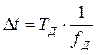– период дискретизации.

Док-во теоремы Котельникова:

,

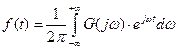где комплексный спектр Фурье: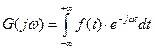

Спектр ограничен, т.е.: 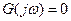при ω > ω_с.

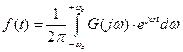
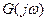в интервале частот (-ω_с, ω_с) можно представить рядом Фурье в экспоненциальной форме:

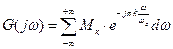, где

коэффициенты ряда Фурье: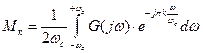

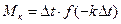- чётная функция

Окончательно:

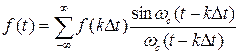
(ω_с= ω_max в спектре) #

Не используется, т. к.:

1-Нет сигналов с ограниченным спектром (бесконечное время накопления информации о сигнале).

2-Нет идеальных фильтров нижних частот (физически не реализуем).