Под кручением понимается такой вид нагружения, когда в поперечных сечениях бруса возникают крутящие моменты. Крутящий момент будем считать положительным, если, глядя со стороны внешней нормали к сечению, наблюдатель видит его направление против часовой стрелки (рис.3.9).
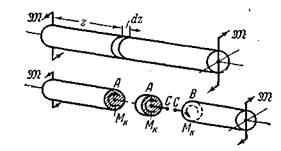 |
Рис. 3.9
Нанесем на боковую поверхность скручиваемого бруса ортогональную сетку (рис. 3.10).
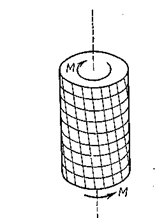
Рис. 3.10
После закручивания прямоугольники перекашиваются. При кручении происходит поворот одного сечения относительно другого. Сформулируем гипотезы, которые положим в основу дальнейших выводов.
1) Сечения, плоские до закручивания, остаются плоскими, и после закручивания.
2) Радиусы, проведенные в любом поперечном сечении, в процессе кручения не искривляются.
Двумя поперечными и кольцевым сечением выделим элемент длиною 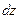 (рис. 3.11).
(рис. 3.11).
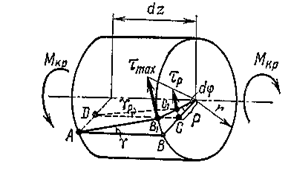
Рис. 3.11
Для удобства левое его сечение будем считать неподвижным. Поворот правого сечения относительно левого равен 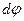 . Образующая
. Образующая 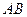 отклонится на малый угол
отклонится на малый угол 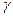 и перейдет в положение
и перейдет в положение 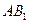 . Угол сдвига волокна, лежащего на поверхности стержня, определяется равенством
. Угол сдвига волокна, лежащего на поверхности стержня, определяется равенством 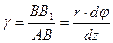 .
.
Для произвольного волокна, отстоящего от центра на расстоянии 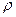
 , будем иметь
, будем иметь 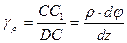 . На основании закона Гука при сдвиге для двух указанных точек можно записать
. На основании закона Гука при сдвиге для двух указанных точек можно записать
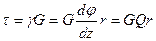 (3.6)
(3.6)
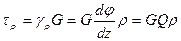 , (3.7)
, (3.7)
где 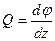 — относительный угол закручивания.
— относительный угол закручивания.
Из формулы видно, что напряжения  меняются по сечению по линейному закону пропорционально радиусу
меняются по сечению по линейному закону пропорционально радиусу  . Графически этот закон представлен на рис. 3.12,а. Для стержня кольцевого сечения закон распределения касательных напряжений показан на рис. 3.12,б.
. Графически этот закон представлен на рис. 3.12,а. Для стержня кольцевого сечения закон распределения касательных напряжений показан на рис. 3.12,б.
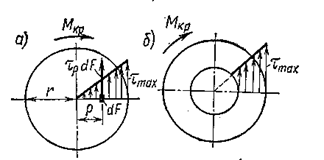
Рис. 3.12
Элементарные силы 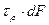 создают крутящий момент
создают крутящий момент
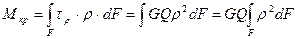 ,
,
Откуда 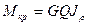 ,
,
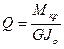 (3.8)
(3.8)
Подставляя в формулу (3.7) полученное выражение (3.8) окончательно получим
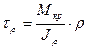 (3.9)
(3.9)
Мы получим формулу для определения 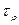 в любой точке поперечного сечения. Максимальные напряжения в крайних точках сечения определяют по формуле
в любой точке поперечного сечения. Максимальные напряжения в крайних точках сечения определяют по формуле
 , (3.10)
, (3.10)
где  — полярный момент сопротивления.
— полярный момент сопротивления.
Взаимный угол поворота двух сечений расположенных на расстоянии 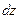 равен
равен 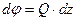 (т.к.
(т.к. 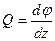 ).
).
С учетом (3.8) получим 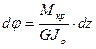 .
.
Абсолютный угол закручивания равен
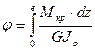 (3.11)
(3.11)
Если 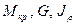 — const, то
— const, то
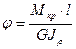 (3.12)
(3.12)
Условия прочности и жесткости при кручении имеют вид
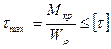 (3.13)
(3.13)
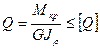 (3.14)
(3.14)
Вычислим полярные моменты инерции и сопротивления для круга и кольца. По определению их значения определяются выражениями
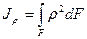 ,
,  .
.
Вырежем тонкое кольцо (рис.3.13).
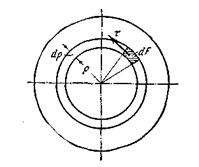
Рис. 3.13
Его площадь 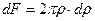 . Подставляя
. Подставляя 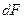 в интервал
в интервал 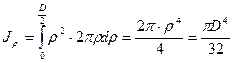 . После вычисления интеграла получим:
. После вычисления интеграла получим: 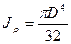 ,
, 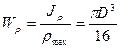 .
.
Для кольцевого сечения (рис.3.14) 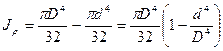 .
.
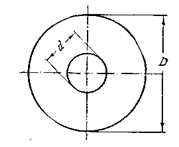
Рис. 3.14
Пусть 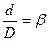 , тогда
, тогда 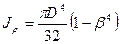 ,
, 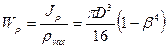 .
.
 2014-02-02
2014-02-02 1727
1727

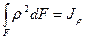 —
— 






