Кручение бруса прямоугольного поперечного сечения

Данная задача является более сложной, чем предыдущая, т.к. здесь не справедлива гипотеза плоских сечений. Отдельные точки сечения перемещаются вдоль оси стержня, и все сечение в целом перестает быть плоским. Происходит так называемая депланация сечения (рис. 3.15).

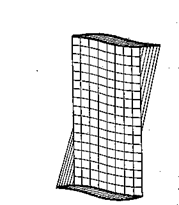
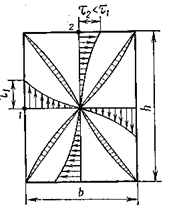
Рис. 3.15 Рис. 3.16

Точное решение данной задачи дается в курсе теории упругости. Здесь приведем только окончательные результаты для стержня прямоугольного сечения. На рис 3.16 приведены эпюры 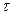для сечений по осям и диагоналям прямоугольного сечения.

Наибольшие касательные напряжения будут в середине длинной стороны прямоугольника.

; .

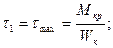
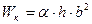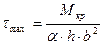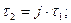причем .

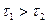Угол закручивания равен

; .

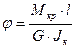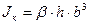Входящие в эти формулы коэффициенты 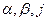зависят от отношения сторон 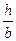и даны в таблице 1.

Таблица 1

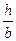		1.5	1.75		2.5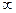
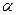	0.208	0.231	0.239	0.246	0.258	0.267	0.282	0.299	0.307	0.313	0.333
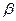	0.141	0.196	0.214	0.229	0.249	0.263	0.281	0.299	0.307	0.313	0.333
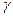	1.000	0.859	0.820	0.795	0.766	0.753	0.745	0.743	0.742	0.742	0.742