Рассмотрим следующие три интеграла (рис. 4.3).
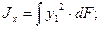
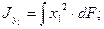

Первые два интеграла называются осевыми моментами инерции сечения относительно осей 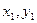 , а третий — центробежным моментом инерции относительно осей
, а третий — центробежным моментом инерции относительно осей 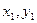 .
.
Пусть заданы: 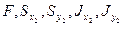 .
.
Требуется найти 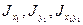 .
.
Координаты площади 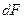 в системе координат
в системе координат 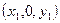 равны:
равны: 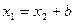
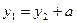 . Вычислим моменты инерции относительно осей
. Вычислим моменты инерции относительно осей 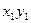 .
.
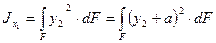 ,
,
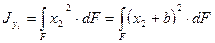 ,
,
 .
.
После интегрирования имеем:
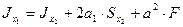 ,
,
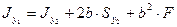 ,
,
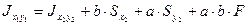 .
.
Если оси 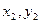 — являются центральными, то
— являются центральными, то 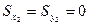 и выражения принимают вид
и выражения принимают вид

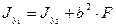
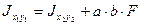 (4.4)
(4.4)
(4.4) называют формулами перехода для моментов инерции от центральных осей 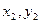 к произвольным
к произвольным 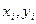 .
.
Из первых двух формул (4.4)следует, что в семействе параллельных осей минимальный момент инерции получается относительно центральной оси (при 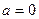 или
или 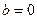 ).
).
Поэтому легко установить, что при переходе от центральных осей к произвольным моменты инерции увеличиваются на 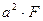 и
и 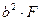 , а при переходе от произвольных к центральным эти величины нужно вычитать.
, а при переходе от произвольных к центральным эти величины нужно вычитать.
При определении центрального момента инерции следует учитывать знак 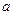 и
и 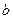 .
.
Пример: Найти моменты инерции прямоугольного относительно основания и относительно центральных осей (рис. 4.4).
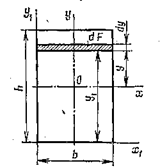
Рис. 4.4
Момент инерции относительно оси 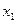
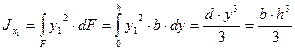 .
.
Воспользуемся формулами переноса (4.4)
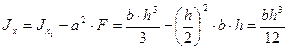 .
.
По аналогии
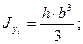
 .
.
Моменты инерции прямоугольника относительно центральных осей необходимо помнить,
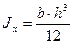
 .
.
 2014-02-02
2014-02-02 1447
1447
