Статические моменты сечения. Возьмем некоторое поперечное сечение бруса (рис

Возьмем некоторое поперечное сечение бруса (рис. 4.2)

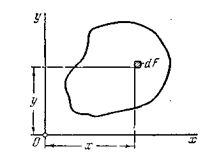
Рис. 4.2

Свяжем его с системой координат 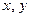и рассмотрим два следующих интеграла

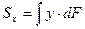
(4.1)

Индекс 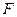у интеграла означает, что интегрирование ведется по всей площади сечения.

Первый интеграл называется статическим моментом сечения относительно оси 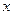, а второй статическим моментом относительно оси 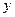. Размерность — .

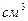При параллельном переносе осей величины статических моментов меняются. Рассмотрим две пары параллельных осе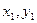й и 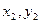(рис. 4.3).

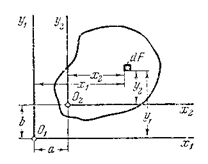
Рис. 4.3

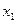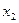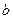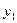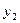Пусть расстояние между осями и равно , а между и равно 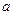. Дано: 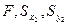. Требуется определить .

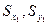Очевидно, что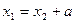

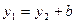
Искомые статические моменты равны

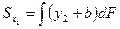
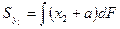
Или .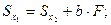

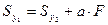Рассмотрим подробнее, например, первое из полученных выражений

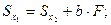
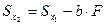
Величина 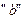может быть как положительной, так и отрицательной. Всегда можно подобрать 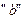так, причем единственным образом, чтобы,

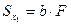, тогда 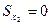. Ось, относительно которой статический момент равен “0”, называется центральной.

Расстояние до центральной оси от некоторой произвольной 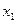равно

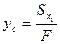, (4.2)

аналогично

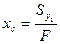. (4.3)

Таким образом, с помощью формул (4.2), (4.3) можно найти центр тяжести любой фигуры.