2014-02-09
1008
ОСНОВЫ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ
ЛЕКЦИЯ №11
Постановка задачи: В пространстве движется объект. Необходимо на его борту в каждый момент времени получать информацию об ориентации, скоростях и координатах этого объекта относительно планеты. А планета движется относительно инерциальной системы отсчета. То есть поставим задачу создания системы, генерирующей в каждый момент времени движения объекта указанную информацию.
Для решения поставленной задачи рассмотрим движения объекта относительно планеты (рис.1).
Введем обозначения:
1. Системы координат и их орты:
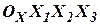- связанная с объектом, 
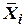- ее орты, 
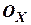- полюс объекта;
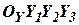- связанная с планетой, 
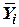- ее орты;
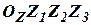- связанная с инерциальной системой отсчета, 
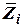- ее орты.
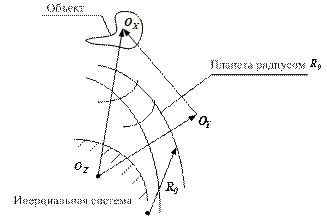
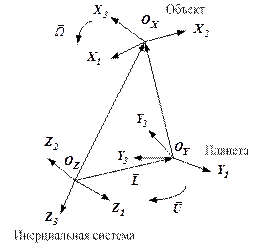
Рисунок 1 Рисунок 2
2. Векторы:
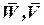- ускорения и скорости полюса относительно инерциальной системы отсчета;
- радиус-вектора полюса объекта относительно начала планетной системы отсчета;
- абсолютная угловая скорость планеты;
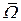- абсолютная угловая скорость объекта;
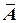- кажущееся ускорение полюса объекта;
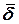- гравитационное ускорение полюса объекта.
3. Проекции векторов (приведены в табл. 1):
Таблица 1
 |  | | | |  | | |
| |  |  |  |  | - |  |  |
| | - |  |  | - |  |  | - |
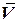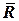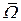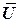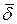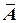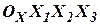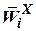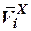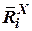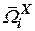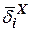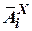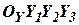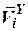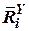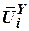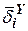4. Направляющие косинусы от планетной системы координат к объектной:
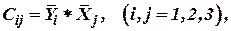 | (1) |
где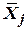 
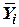, - орты соответственно координатных осей , .
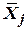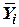5. Начальные условия:
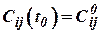- значение направляющих косинусов в начальный момент времени 
;
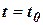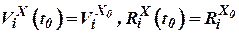- значение проекций векторов 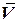, 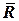на сои системы координат .
Применив операцию абсолютного дифференцирования по времени (АДВ) к равенству (1), получим:
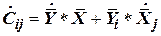 , | (2) |
где 
обозначена операция АДВ. Таким образом, орт принадлежит планетной системе координат, вращающийся относительно инерциальной системы отсчета с угловой скоростью , а орт 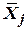принадлежит объектной системе координат вращающийся относительно инерциальной с угловой скоростью 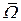, то
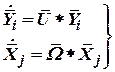 | (3) |
Подставим (3) в (1) получим
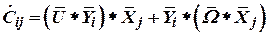 . | (4) |
Вектор 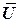задан проекциями в планетной системе координат, а вектор 
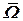представим через проекции в объектной системе координат
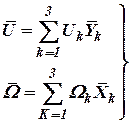 . | (5) |
Подставив (1) в (4), получим
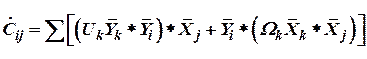 . | (6) |
Используя (1), составим выражение
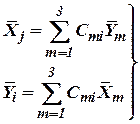 . | (7) |
Подставив (7) в (6) получим
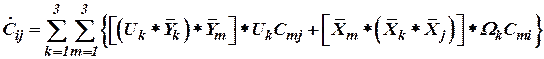 . | (8) |
Используя символ Леви-Чивита
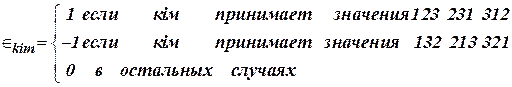 , | (9) |
перепишем (8)
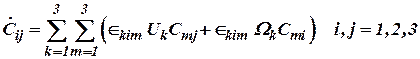 . | (10) |
По определению кинематики:
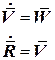 . | (11) |
Использовав определение кажущегося ускорения полюса объекта
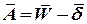 | (13) |
где 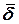- гравитационное ускорение.
С учетом (13), перепишем (11) так
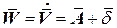 . | (14) |
Задав векторы 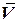,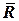в объектной системе координат, вращающиеся относительно инерциальной с угловой скоростью 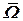, запишем 
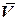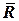, и получим уравнения
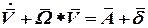 ; | (15) |
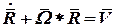 , | (16) |
где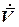 
,
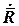- локальные производные по времени в объектной системе координат.
Перепишем (15), (16) в виде
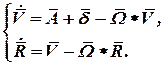 | (17) (18) |
При сферическом поле тяготения планеты силовая функция этого поля имеет вид
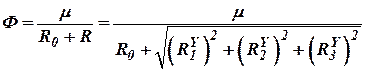 | (19) |
где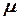 
- константа, равная произведению массы планеты на ее гравитационную постоянную;
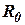- радиус планеты.
Тогда вектор 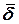определяется выражением
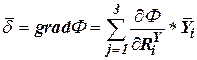 , | (20) |
где в силу (19)
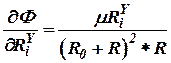 , | (21) |
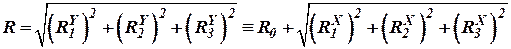 . | (22) |
Подставим (21) в (22) получим
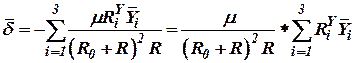 . | (23) |
Так как
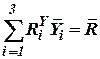 , | (24) |
то
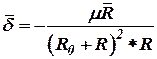 . | (25) |
Обозначим
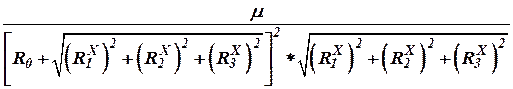 | (26) |
и заметим, что это функция переменных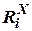 
. Используя (25), перепишем (26)
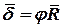 . | (27) |
Спроектировав (27) на оси системы координат 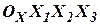, получим его в скалярной форме
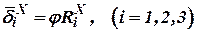 | (28) |
Итак, при сферическом поясе тяготения планеты проекции вектора гравитационного ускорения полюса объекта на оси объектной системы координат являются нелинейными функциями проекций радиуса-вектора полюса объекта на оси этой же системы координат.
Запишем векторные уравнения (17), (18) в скалярной форме. Для этого умножим каждое из них на орт 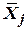и получим
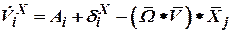 ; | (29) |
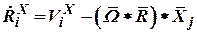 . | (30) |
Векторы 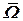, , 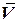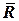заданы проекциями в объектной системе координат, поэтому (29), (30) перепишем в виде
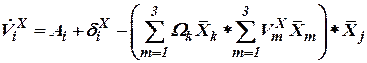 , | (31) |
 . | (32) |
Используя символ Леви-Чивита (9), перепишем (31), (32)
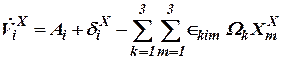 , | (33) |
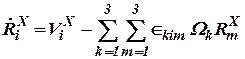 . | (34) |
Векторы 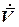, 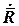представляются выражением через их проекции на оси объектной системы координат.
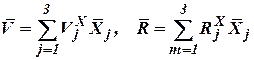 | (35) |
Умножив каждое из этих выходных равенств на орт 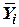скалярно и использовав (1), получим
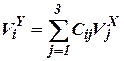 | (36) |
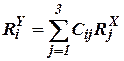 | (37) |
Итак, получены уравнения (10), (33), (34), формулы (26) и зависимости (28), (36), (37) позволяющие указать состав системы, генерирующий на борту объекта информацию о его ориентации, скоростях и координатах в пространстве.
Эта система должна, во первых, генерировать в каждый момент времени информацию о проекциях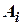 
, 
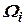векторов 
, 
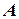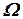. Во вторых, она должна запомнить информацию о гравитационном поле (величины 
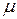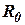, или силовую функцию 
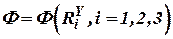) и проекции 
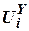вектора 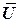угловой скорости планеты. В третьих, она должна иметь информацию о начальных условиях 
, 
, 
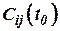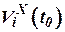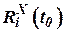. В четвертых, эта система должна иметь в своем составе вычислительное устройство, способное решать дифференциальные уравнения (10), (33), (34) в реальном масштабе времени.
Описанная система, в которой информация о проекциях 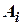, 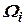генерируется на инерциальной навигационной системе (ИНС).
Обобщенная блок-схема ИНС
Введем некоторые понятия и определения.
· положение объекта в пространствебудем определять координатами его полюса относительно базовой системы координат.
· движение объекта в пространстве будем определять проекциями вектора скорости его полюса на оси объектной или базовой системы координат.
· ориентацию объекта в пространстве будем определять направляющими косинусами от базовой к объектной системе координат.
· навигационной информацией (НИ) называется совокупность переменных, определяющих положение, движение и ориентацию объекта в пространстве в каждый момент времени.
· априорной информацией (АИ) называется совокупность величин и функций, определяющих гравитационное поле, вращение планеты и значение навигационной информации в начальный момент времени.
· измеряемой информацией (ИИЗМИ) называется совокупность выходных сигналов инерциальных датчиков и других датчиков.
· инерциальной информацией (ИНИ) называется совокупность шести скалярных переменных, три из которых определяют поступательное движение, другие три – его угловое движение чаще всего, это три проекции вектора кажущегося ускорения полюса объекта и три проекции вектора его абсолютной угловой скорости на оси объектной системы координат.
· алгоритм функционирования ИНС называется последовательность измерительных и вычислительных операций выполнение которых позволяет получить навигационную информацию.
На рис.3 изображена обобщенная блок-схема ИНС, где указаны следующие блоки:
| - блок хранения априорной информации (АИ); | |
| - блок измеряемой информации (ИИЗМИ); | |
| - блок инерциальной информации (ИНИ); | |
| - блок навигационной информации (НИ); | |
| - базовое вычислительное устройство (БВУ); | |
| - источник энергии (ИЭ). |
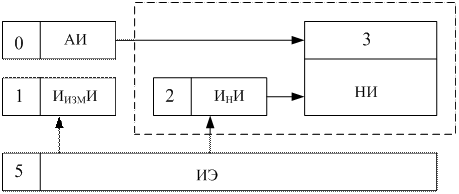
Рисунок 3
Блок «0» хранение априорной информации – это ЗУ БЦВМ.
Блок «1» измеряемой информации – это блок инерциальных – это блок инерциальных датчиков и других датчиков, генерирующих или непосредственно дающих инерциальную информацию, или информацию, позволяющую ее вычислить.
Блок «2» инерциальной информации – это или встроенный в блок 1 специальное вычислительное устройство или часть БЦВМ, обрабатывающая измеряемую информацию с целью получения инерциальной информации.
Блок «3» навигационной информации – это БВУ, в котором на основе априорной и инерциальной информации вычисляется навигационная информация.
Источник энергии «5» необходим для обеспечения работоспособности блоков 1-4.
